Questões de Estatística do ano 2011

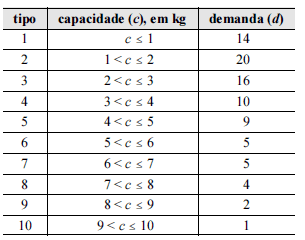
Considere que determinado fabricante classifique suas embalagens de acordo com a capacidade de armazenamento unitário (c), em kg, de determinado produto — por exemplo, a embalagem do tipo 10 permite armazenar mais de 9 e até 10 kg do produto. Com base nessas informações e na tabela acima, que mostra a distribuição dos dez tipos de embalagens e a demanda observada em março de 2011 para cada tipo, julgue os itens que se seguem.

Um quarto da demanda foi por embalagens com capacidades para mais de 4 kg.

• C. Certo
• E. Errado

Para responder às questões de números 68 e 69, considere a seguinte distribuição de frequência (considere os intervalos de classe abertos à esquerda e fechados à direita):

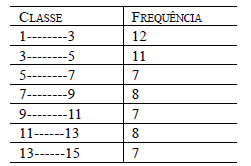
Assinale a alternativa que contém uma afirmação verdadeira.

• A.

  A mediana é 7.

• B.

  A distribuição é simétrica.

• C.

  A distribuição acumulada abaixo da quarta classe é 22.

• D.

  A moda situa-se na quarta classe.

• E.

  O desvio padrão é 8.

Foi selecionada uma amostra de 200 estudantes, e foram pesquisadas as variáveis X = fazer cursinho e Y = passar no vestibular. Os resultados estão na tabela seguinte:

Pela tabela, pode-se concluir que

• A.

  entre os que fizeram cursinho, 80% foram aprovados.

• B.

  entre os que não fizeram cursinho, 60% foram reprovados.

• C.

  dessa amostra, 60% foram reprovados.

• D.

  dessa amostra, 80% fizeram cursinho.

• E.

  entre os reprovados, 40% não fizeram cursinho.

O quadro acima mostra a forma de cálculo do índice de desenvolvimento humano (IDH) divulgado periodicamente pelo PNUD. O índice é calculado para cada país participante, e os 169 países participantes são agrupados em quatro categorias de desenvolvimento humano. Um país estará no grupo muito elevado se o seu IDH estiver no quartil superior; no grupo elevado, se o seu IDH estiver nos percentis 51–75; no grupo médio, se o seu IDH estiver nos percentis 26–50; e no grupo baixo, se o seu IDH estiver no quartil inferior. Com base nessas informações, julgue os próximos itens.

Políticas de educação podem não causar impacto no IDH de um país.

• C. Certo
• E. Errado

A tabela a seguir apresenta as temperaturas de fusão e ebulição de algumas substâncias. Observe.

Marque a alternativa correta.

• A.

  A tabela apresenta 4 números inteiros e 4 números naturais.

• B.

  A substância Z apresenta a menor temperatura de fusão.

• C.

  A substância que apresenta maior diferença entre suas temperaturas de fusão e ebulição é a substância Q.

• D.

  A temperatura de fusão da substância W é maior que a temperatura de fusão da substância K.

• E.

  A temperatura de fusão da substância T é menor que a temperatura de ebulição da substância X.

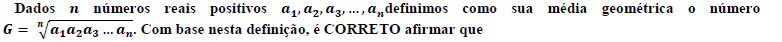
• A.

  se�� e �� são números reais positivos cuja média aritmética é igual à média geométrica, então �� = ��

• B.

  se�� e �� são números reais positivos quaisquer cuja média aritmética é igual a �� e cuja média geométrica é igual a ��, então, necessariamente, �� > ��

• C.

  se�� e �� são números reais positivos quaisquer cuja média aritmética é igual a �� e cuja média geométrica é igual a ��, então, necessariamente, �� = ��

• D.

  se�� e �� são números reais positivos, tais que �� + �� é um número inteiro e par então, necessariamente, tanto a média aritmética quanto a média geométrica desses números serão também números inteiros e pares.

• E.

  se�� e �� são números reais positivos, tais que �� + �� é um número inteiro e ímpar então, necessariamente, tanto a média aritmética quanto a média geométrica destes números serão também números inteiros e ímpares.

Clara e Pedro fizeram um curso de informática e, para serem aprovados, devem ter a média aritmética de sua notas no mínimo igual a 7. As notas de Clara foram 7 ; 5,5 e 8,5; e as de Pedro foram 6,5 ; 4,5 e 8,5. Assinale a resposta CORRETA com a média aritmética de cada um e a situação aprovado ou reprovado, respectivamente.

• A.

  Clara: média 6,5/reprovada e Pedro média 7,0/aprovado.

• B.

  Clara: média 6,0/reprovada e Pedro média 7,0/aprovado.

• C.

  Clara: média 7,0/aprovada e Pedro média 6,5/reprovado.

• D.

  Clara: média 7,5/aprovada e Pedro média 7,5/aprovado.

Com relação aos valores destes salários, a soma da média aritmética com a mediana e com a moda é igual a

• A.

  R$ 11.375,00.

• B.

  R$ 10.875,00.

• C.

  R$ 10.500,00.

• D.

  R$ 10.375,00.

• E.

  R$ 9.675,00.

Para resolver as questões de números 41 e 42 considere uma amostra aleatória com 10 pares de observações (X_i, Y_i), i = 1, 2, . . ., 10. O objetivo é descrever Y como função linear de X por meio do modelo Y_i = α + βX_i + ∈_i, sendo i a i-ésima observação, α e β são parâmetros desconhecidos e ∈i o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Utilizando o método dos mínimos quadrados, obteve-se a e b, que são as estimativas de α e β, respectivamente. Verificou-se que a reta determinada pela função Y = a + bX passa pelos pontos (1, 8 ) e (4 , 2).

Se o valor da média das observações Y_i é igual a 4,4; então, a média das observações X_i é

• A.

  3,6.

• B.

  3,2.

• C.

  2,8.

• D.

  2,4.

• E.

  2,0.

A respeito de regra de três simples e composta, proporções e média aritmética, julgue os itens a seguir.

Considere que, para um aluno ser aprovado em matemática, a média aritmética das suas notas parciais deva ser igual ou superior a 5,0. Nesse caso, se as notas parciais desse aluno, nessa disciplina, forem 8,0; 6,5; 6,0; 3,5; 2,5; 5,0; e 4,0, então esse aluno será aprovado em matemática.

• C. Certo
• E. Errado