Questões de Estatística do ano 2011

A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.

A média e a mediana do número de eleitores que não votaram estão entre 4.000 e 6.000.

• C. Certo
• E. Errado

Em um período de 200 dias úteis, observou-se em uma repartição pública a autuação de processos apresentando uma certa característica. A fórmula f_k = 10 + 45 K − 10 K² fornece a informação do número de dias úteis (f_k) em que se verificou a autuação de K destes processos, sendo que K assume somente os valores 0, 1, 2, 3 e 4. Calculando, para o período considerado, os respectivos valores da média aritmética (quantidade de processos autuados por dia), da mediana e da moda, a soma destes 3 valores é

• A.

  7,75.

• B.

  7,25.

• C.

  6,75.

• D.

  6,50.

• E.

  6,25.

Em uma classe com 20 alunos, foram anotados, na tabela, o sexo e a nota de cada um.

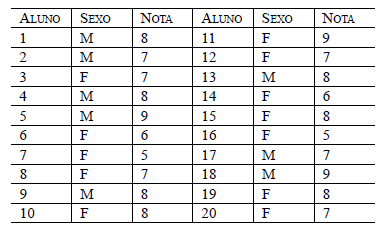
Após fazer as distribuições de frequência das notas, é possível concluir que

• A.

  60% da classe é do sexo masculino.

• B.

  a média dos alunos do sexo masculino é superior à média das alunas.

• C.

  entre os alunos do sexo masculino, a moda é 7.

• D.

  entre as alunas, a mediana é 8.

• E.

  entre todos os alunos, a moda é 7.

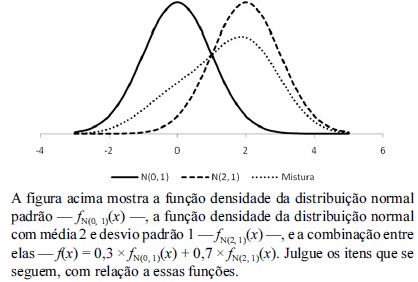
A moda da distribuição da combinação f(x) coincide com a moda de f_{N(0, 1)}(x) ou com a moda de f_{N(2, 1)}(x).

• C. Certo
• E. Errado

O valor da moda (Mo), obtido pela relação de Pearson: Mo = 3Md − 2Me , é igual a

• A.

  R$ 4.250,00.

• B.

  R$ 4.500,00.

• C.

  R$ 4.750,00.

• D.

  R$ 5.000,00.

• E.

  R$ 5.250,00.

Da fórmula Sturges infere-se que a moda dessa distribuição é inferior a 75 kg.

• C. Certo
• E. Errado

Considerando-se duas variáveis aleatórias contínuas X e Y, em que X tem função de densidade arbitrária f com função geradora de momentos M(t) e Y = exp(X), julgue os próximos itens.

E(Y) = exp[E(X)].

• C. Certo
• E. Errado

Os aposentos de um hotel internacional estão distribuídos em corredores com uma dúzia de apartamentos de cada lado. Um dos corredores está com os apartamentos ocupados, exceto um deles, que fica no meio do corredor. Um hóspede chega ao hotel e será acomodado naquele aposento. Se os hóspedes já acomodados naquele corredor forem redistribuídos aleatoriamente no mesmo corredor, e, exatamente, dez deles tiverem a mesma nacionalidade do hóspede que será acomodado agora, então a probabilidade de que os três vizinhos — à esquerda, à direita e à frente — do novo hóspede sejam seus compatriotas é

• A.

  menor que 5%.

• B.

  maior que 5%, mas menor que 10%.

• C.

  maior que 10%, mas menor que 15%.

• D.

  maior que 15%, mas menor que 20%.

• E.

  maior que 20%.

Dado um conjunto finito ��, chamamos de conjunto das partes de ��ou 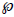��) ao conjunto cujos elementos são todos os subconjuntos de ��. Com base nesta definição, é CORRETO afirmar que

• A.

  ∅é elemento de  �� , se, e somente se for elemento também de ��.

• B.

  ∅é elemento de  �� , qualquer que seja o conjunto ��.

• C.

  {∅}é elemento de ��, ) se, e somente se, for elemento também do conjunto ��.

• D.

  {∅}jamais pode ser elemento de  �� , pois �� é assumido como conjunto finito.

• E.

  Se �� ≠ ∅, então {∅} é elemento de (��)

Placas de um circuito integrado são expedidas em lotes de 10 unidades. Antes de um lote ser aprovado um procedimento de controle de qualidade escolhe aleatoriamente e sem reposição 4 placas do lote. Se uma ou mais forem defeituosas, todo o lote é inspecionado. Supondo que num lote haja duas placas defeituosas, a probabilidade de que o controle de qualidade indique uma inspeção de todo o lote é

• A.

  1/3

• B.

  2/3.

• C.

  1/5.

• D.

  2/5.

• E.

  1/4.