Questões de Estatística do ano 2013

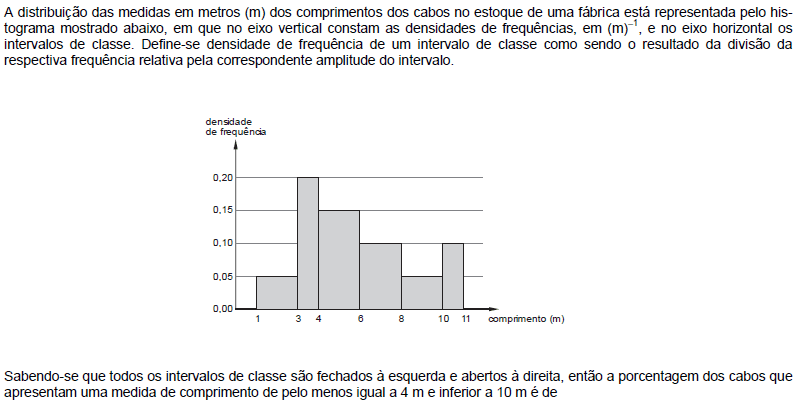
• A. 50%.
• B. 60%.
• C. 70%.
• D. 80%.
• E. 90%.

• A. Me = Md = Mo.
• B. Me = Md e Mo > Me.
• C. Md < Mo < Me.
• D. Me < Md < Mo.
• E. Md < Me < Mo.

Em um órgão público, verifica-se que a média aritmética dos salários dos funcionários com nível superior supera a média aritmética dos restantes dos funcionários em R$ 2.000,00. Sabe-se que o desvio padrão dos salários dos funcionários com nível superior é igual a R$ 500,00 e dos restantes dos funcionários é igual a R$ 300,00, com os respectivos coeficientes de variação iguais. Se 40% dos funcionários possuem nível superior, então a média aritmética dos salários de todos os funcionários deste órgão público é igual a

• A. R$ 3.500,00.
• B. R$ 3.200,00.
• C. R$ 3.600,00.
• D. R$ 3.800,00.
• E. R$ 3.900,00.

• A. c < 21,0%.
• B.
• C.
• D.
• E.

Uma variável aleatória contínua X tem média 20 e, pelo Teorema de Tchebichev, a probabilidade mínima de que pertença ao intervalo (19, 21) é igual a 84%. A variância de X é igual a

• A. 0,16.
• B. 0,25.
• C. 0,40.
• D. 1,00.
• E. 0,64.

Considere que E = (m−1)X − mY + 2Z corresponde a uma classe de estimadores não viesados da média μ de uma população normalmente distribuída com variância σ² ≠ 0. (X, Y, Z) é uma amostra aleatória, com reposição, desta população com m sendo um parâmetro real. O estimador mais eficiente desta classe apresenta uma variância igual a

• A. 2,5 σ².
• B. 3,0 σ².
• C. 4,5 σ².
• D. 5,0 σ².
• E. 6,0 σ².

• A. 65,00%.
• B. 50,00%.
• C. 48,75%.
• D. 32,50%.
• E. 16,25%.

Considere uma variável aleatória X uniformemente distribuída no intervalo (m, n) em que nem m e nem n são conhecidos. Com base em uma amostra aleatória de tamanho 10 obteve-se que os valores do primeiro e do segundo momentos da amostra foram, respectivamente, 1,00 e 1,12. Aplicando o método dos momentos, tem-se que as estimativas de m e n são, respectivamente,

• A. 0,30 e 1,70.
• B. 0,40 e 1,60.
• C. 0,50 e 1,50.
• D. 0,60 e 1,40.
• E. 0,70 e 1,30.

Em 100 experiências realizadas ao acaso, independentemente, para apurar o valor de uma constante física, obteve-se uma média de 3,7 para esta constante. Admite-se que a distribuição da população dos resultados é normalmente distribuída, de tamanho infinito, com média μ e com uma variância populacional igual a 0,16. Considere na curva normal padrão (Z) as probabilidades P(Z > 1,64) = 0,05 e P(Z > 1,96) = 0,025. Com base na amostra inicial de 100 experiências, obtém-se que o intervalo de confiança ao nível de 95% para μ é

• A. [3,6344 ; 3,7656].
• B. [3,6280 ; 3,7720].
• C. [3,6216 ; 3,7784].
• D. [3,6152 ; 3,7848].
• E. [3,6088 ; 3,7912].

Em uma empresa com grande número de empregados, realizou-se uma pesquisa com 150 deles escolhidos aleatoriamente, com reposição, perguntando a cada um se estava satisfeito com o novo presidente do sindicato de sua categoria. A pesquisa revelou que 90 empregados estavam satisfeitos. Considere que é normal a distribuição amostral da frequência relativa dos empregados satisfeitos com o novo presidente e que na curva normal padrão (Z) têm-se as probabilidades P(Z > 1,64) = 0,05 e P(Z > 1,28) = 0,10. O intervalo de confiança para esta proporção ao nível de 90%, com base no resultado da amostra, apresenta um limite inferior igual a

• A. 53,44%.
• B. 54,16%.
• C. 54,88%.
• D. 56,72%.
• E. 57,14%.