Questões sobre Estimação e Intervalo de Confiança

Um pesquisador da área de saúde está testando uma nova fórmula para um medicamento antitérmico. Ele acredita que a nova fórmula forneça um tempo de reação mais rápido que a fórmula antiga. São desconhecidas a média e a distribuição de probabilidade desse tempo, mas a variância, por analogia a outros medicamentos, é considerada igual a 50. Uma amostra de 500 voluntários que tomaram o novo medicamento resultou num valor médio observado de 25 minutos. O intervalo de confiança [24,38 ; 25,62], para o tempo médio de reação do medicamento, tem nível de confiança de:

• A.

  92%

• B.

  99%

• C.

  96%

• D.

  95%

• E.

  97%

Considere que o tempo de vida de um componente eletrônico é normalmente distribuído com desvio padrão de 10 horas. Sabendo-se que o mesmo tem confiabilidade igual a 97,5% de operar por um período de 100 horas, então, a vida média do componente eletrônico é igual a:

• A.

  116,5 horas

• B.

  119,6 horas

• C.

  123,3 horas

• D.

  125,8 horas

Ao estimar a proporção de consumidores descontentes com a atuação de determinada empresa de telefonia, um pesquisador obteve o erro padrão da proporção igual a 2%. Sabendo-se que 80% dos consumidores pesquisados estão descontentes com a empresa de telefonia, podemos afirmar que o número total de consumidores pesquisados foi igual a:

• A.

  100

• B.

  200

• C.

  400

• D.

  800

Ao estimar o tempo médio (em horas) para a realização de auditorias externas, um analista obteve, a partir de uma amostra de tamanho 36, o seguinte intervalo:

Podemos afirmar que o desvio padrão do tempo para a realização de auditorias externas é igual a:

• A.

  9 horas

• B.

  12 horas

• C.

  15 horas

• D.

  18 horas

O gestor de Marketing de uma empresa deseja estimar, com nível de confiança de 95%, a proporção de clientes cadastrados que praticam algum tipo de atividade esportiva. O tamanho mínimo da amostra, para que o erro da estimativa seja 3,5% é igual a:

• A.

  784

• B.

  1.205

• C.

  365

• D.

  283

Uma grande empresa possui as fichas cadastrais dos seus 8.000 funcionários. Verificou-se que em 100 fichas escolhidas aleatoriamente, 10 estavam com erros no preenchimento. Pode-se afirmar, ao nível de significância de 1%, que a proporção de fichas com erros de preenchimento para todos os funcionários (o valor crítico para o teste é )

• A.

  é superior a 4%

• B.

  é superior a 4%

• C.

  é superior a 6%

• D.

  é superior a 7%

O estatístico responsável pelo controle de qualidade em uma linha de produção de uma usina siderúrgica necessita construir uma carta para controlar a espessura de uma determinada chapa de aço. Então, coletou uma amostra com tamanho de 30 chapas que forneceu as seguintes estatísticas: média amostral de 3,0 mm e coeficiente de variação de 0,005. O estatístico fixou um erro b, um desvio crítico ks, onde s é o desvio padrão e k um real positivo e com essas estatísticas determinou o tamanho da amostra a ser tomada a instantes predefinidos, que foi de 5. Assim, é correto afirmar que a carta de controle da média a três sigmas é composta por:

• A.

  Uma linha central na média LC = 3,00 mm; o limite inferior de controle em LIC = 2,955 mm e o limite superior de controle em 3,045 mm

• B.

  Uma linha central na média LC = 3,00 mm; o limite inferior de controle em LIC = 2,985 mm e o limite superior de controle em 3,15 mm

• C.

  Uma linha central na média LC = 3,00 mm; o limite inferior de controle em LIC = 1,659 mm e o limite superior de controle em 4,341 mm

• D.

  Uma linha central na média LC = 3,00 mm; o limite inferior de controle em LIC = 2,995 mm e o limite superior de controle em 3,005 mm

Em uma pesquisa de tributos de competência estadual, em 2008, realizada com 400 recolhimentos escolhidos aleatoriamente de uma população considerada de tamanho infinito, 80% referiam-se a determinado imposto. Deseja-se construir um intervalo de confiança de 95,5% para a estimativa dessa proporção. Considerando normal a distribuição amostral da frequência relativa dos recolhimentos desse imposto e que na distribuição normal padrão a probabilidade P (−2 ≤ Z ≤ 2) = 95,5%, o intervalo é

• A.

  [0,70; 0,90]

• B.

  [0,72; 0,88]

• C.

  [0,74; 0,86]

• D.

  [0,76; 0,84]

• E.

  [0,78; 0,82]

Certo distribuidor, ao comercializar um novo aditivo, assegura que este faz reduzir o consumo de combustível. Com o objetivo de testar tal afirmação, selecionou-se uma amostra aleatória de 36 carros de diversos modelos, que fizeram o mesmo percurso, nas mesmas condições, com o combustível sem aditivo e depois, com aditivo. A média da diferença entre o consumo (sem aditivo menos com aditivo) fornecido pela amostra foi de 0,2 litros e desvio padrão amostral de 0,01 litros de combustível. Como o p-valor desse teste é aproximadamente 0,10%, nos níveis de 1%, 5% e 10% de significância, respectivamente, conclui-se que o novo aditivo

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

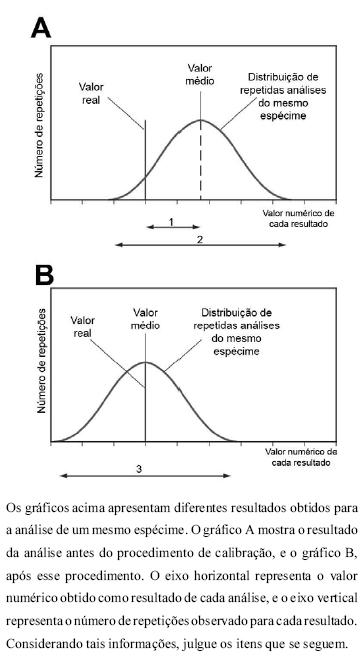
No gráfico A, a seta indicada por 1 mostra que o valor médio dos resultados antes da calibração ocorria com freqüência menor que o valor real.

• C. Certo
• E. Errado