Questões sobre Medidas de Posição Central

Considere as informações abaixo correspondentes a uma distribuição estatística, determinando uma curva de frequência unimodal:

I. Uma medida de curtose tem como objetivo determinar o desvio ou afastamento da simetria da respectiva curva de frequência.

II. Se a moda for menor que a mediana e a mediana menor que a média, então, a distribuição de frequência correspondente é assimétrica à direita.

III. Se a média for menor que a mediana e a mediana menor que a moda, então, a distribuição de frequência correspondente é assimétrica à esquerda.

IV. Se a curva de frequência correspondente for caracterizada como leptocúrtica, então, a moda é superior à média e à mediana.

Está correto o que consta APENAS em

• A.

  I e II.

• B.

  I e III.

• C.

  II e III.

• D.

  II e IV.

• E.

  II, III e IV.

Com base nessas informações, julgue os itens a seguir.

A mediana dos dados é maior ou igual a 3.

• C. Certo
• E. Errado

0 0 3 3 3 4 1 2 2 1 1 2 3 3 4 1 2 2 0 4

Considerando os dados acima, que representam a quantidade de doutores presentes em pesquisas que geraram patentes industriais, julgue os próximos itens.

A mediana dos dados é igual a 3.

• C. Certo
• E. Errado

Em um experimento, obteve-se uma amostra de 15 valores da variável discreta x. A amostra é dada pelo conjunto {1, 2, 3, 1, 3, 4, 3, 4, 3, 2, 3, 5, 2, 4, 5}. Assim, para esta amostra, a média aritmética, a moda, a mediana e o tipo de distribuição obtidas são, respectivamente:

• A.

  3, 5, 3, assimétrica positiva

• B.

  3, 5, 3, assimétrica negativa

• C.

  3, 5, 3, simétrica

• D.

  3, 3, 3, simétrica

• E.

  3, 3, 5, assimétrica negativa

Ricardo fez 6 concursos públicos em cujas provas obteve as seguintes notas: 6,6; 6,6; 8,2; 7,8; 4,3; 9,1. A média, a moda e a mediana das notas de Ricardo são, respectivamente:

• A.

  7,2; 6,6; 8.

• B.

  8; 6,6; 7,2.

• C.

  8; 7,2; 7,1.

• D.

  6,6; 7,1; 8.

• E.

  7,1; 6,6; 7,2.

Foram observadas 10 realizações independentes de uma variável aleatória X, as quais, depois de ordenadas, são: 1, 1, 2, 4, 4, 4, 5, 5, 6, 6. Nesta amostra, a(o)

• A.

  média é 4.

• B.

  moda é 4.

• C.

  variância é maior que 25.

• D.

  covariância é 3.

• E.

  desvio padrão é maior que 5.

O Teorema Central do Limite afirma que quando o tamanho de uma amostra aumenta, a distribuição das médias amostrais converge para uma distribuição:

• A.

  qui-quadrado.

• B.

  F de Fisher-Snedecor.

• C.

  normal.

• D.

  t de Student.

• E.

  ognormal.

Considere o seguinte conjunto de dados composto por cinco elementos: {82,93; 94,54; 98,40; 115,41; 123,07}.

Com base nesses dados, julgue os itens subsequentes acerca das medidas de tendência central.

A média do conjunto de dados em questão é 102,87 e a mediana é 98,40. Se o valor 123,07 for alterado para 200, a média irá aumentar, mas a mediana continuará sendo 98,40.

• C. Certo
• E. Errado

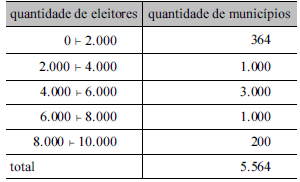
A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.

A moda da distribuição se encontra no mesmo intervalo de classe que contempla a mediana e a média.

• C. Certo
• E. Errado

A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.

A média e a mediana do número de eleitores que não votaram estão entre 4.000 e 6.000.

• C. Certo
• E. Errado