Questões sobre Probabilidade

Considerando A e B dois eventos aleatórios, com probabilidades P(A) = 0,4 e P(B) = 0,1, e o evento complementar B^c, julgue os itens seguintes, relativos a probabilidade condicional. Em face dos dados apresentados, é correto afirmar que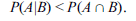

• C. Certo
• E. Errado

Considerando A e B dois eventos aleatórios, com probabilidades P(A) = 0,4 e P(B) = 0,1, e o evento complementar B^c, julgue os itens seguintes, relativos a probabilidade condicional. Considerando-se que A e B sejam eventos mutuamente excludentes, é correto afirmar que P(A|B^c ) = 0.

• C. Certo
• E. Errado

Um dos frascos do xarope, na referida amostra, foi coletada aleatoriamente e a quantidade de Escherichia coli foi anotada. Outra unidade foi selecionada por apresentar turvação e verificou-se tratar do produto com maior quantidade de Escherichia coli. Procedeu-se então à coleta aleatória de uma terceira unidade. Na primeira seleção, considera-se “X” a probabilidade de que a unidade do xarope selecionada tenha quantidade de Escherichia coli maior do que 5 UFC/mL. Já na coleta da terceira unidade, considera-se “Y” a probabilidade de que essa amostra apresente quantidade de Escherichia coli menor do que 5 UFC/mL. Verifica-se que a primeira unidade selecionada apresentou quantidade de Escherichia coli igual a 6 UFC/mL.

Sabendo-se que, no processo de coleta aleatória, todas as unidades do xarope possuem a mesma probabilidade de serem selecionadas, então, os valores de “X” e “Y” são, respectivamente

• A.

  50% e 44%.

• B.

  50% e 50%.

• C.

  60% e 40%.

• D.

  50% e 40%.

• E.

  44% e 50%.

A quantidade diária de reclamações — X — recebidas em uma central de atendimento ao consumidor segue uma distribuição de Poisson, em que P(X = 0) = 0,5. Nesse sentido, julgue os próximos itens.

A probabilidade condicional P(X = 1*X > 0) é igual à variância de X.

• C. Certo
• E. Errado

A distribuição condicional Y3*{X₀ = 0, X₁ = 0, X₂ = 0} é uma distribuição de Bernoulli cuja probabilidade de sucesso é 0,9.

• C. Certo
• E. Errado

Um rato está preso no labirinto (veja a representação na figura a seguir), onde há vários caminhos distintos que o levam até a comida (queijo). O rato escolhe cada porta de maneira aleatória.

Qual é a probabilidade de que o rato consiga pegar o queijo?

• A. 1/18
• B. 1/12
• C. 1/5
• D. 119/120
• E. 119/240

A probabilidade de que João seja parado para fazer o teste do bafômetro, em uma blitz da polícia, é de 10 % todos os dias quando volta para casa. Qual é a probabilidade de que ele seja parado nessas blitze mais de 15 vezes ao longo de 100 dias?

• A. Menos de 1,0 %.
• B. Entre 1,5 % e 3,0%
• C. Entre 3,5 % e 5,5 %.
• D. Entre 6,5 % e 8,5 %.
• E. Mais de 10 %.

O tempo de ligações telefônicas segue uma distribuição de probabilidade exponencial com média de 3 minutos. Um sujeito chega a um telefone público e descobre que a pessoa à sua frente está na ligação há pelo menos dois minutos.

Qual é a probabilidade de essa ligação durar pelo menos cinco minutos no total?

• A.

  e⁻¹

• B.

  e⁻²

• C.

  e⁻³

• D.

  1 − e⁻³

• E.

  1 − e⁻⁵

Suponha que determinado servidor público esteja revisando um texto de 10 páginas e que cada página contenha 36 linhas completamente digitadas. Considere ainda que, ao revisar o texto, o servidor encontre em média um erro tipográfico a cada 4 linhas revisadas. Com base nessas informações, julgue os itens seguintes.

Se, antes de fazer a revisão, o servidor tivesse escolhido aleatoriamente 3 linhas diferentes em qualquer das páginas para verificar se essas linhas continham erros, a probabilidade de que nenhuma dessas linhas contivesse erros tipográficos seria de 9/16.

• C. Certo
• E. Errado

Dentro de um saco há 24 balas, todas indistinguíveis, a não ser por seus sabores: 6 são de morango, 8 de caramelo e 10 de hortelã. Uma pessoa coloca a mão dentro do saco e pega n balas.

Para que essa pessoa tenha certeza de que pegou pelo menos duas balas de hortelã, o menor valor de n deverá ser

• A.

  4

• B.

  10

• C.

  16

• D.

  18

• E.

  20