Questões sobre Probabilidade
Lista completa de Questões sobre Probabilidade para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Considerando os conceitos associados a probabilidade e estatística, julgue os itens de 108 a 116. Considere que de uma urna contendo 2 bolas azuis e 6 bolas brancas retira-se ao acaso uma bola, anota-se sua cor e repõe-se a bola na urna. Em seguida retira-se novamente uma bola da urna e anota-se sua cor. Nessas condições, a probabilidade das duas bolas retiradas serem azuis é 1/4.
- C. Certo
- E. Errado
Considerando a matriz de transição 
, julgue os próximos itens acerca de cadeias de Markov.
O vetor de distribuição do processo no limite estacionário é 
- C. Certo
- E. Errado
Considerando os conceitos associados a probabilidade e estatística, julgue os itens de 108 a 116. Considere que as bolas de uma urna tenham sido divididas em duas caixas, sendo que a caixa I ficou com 3 bolas brancas e 1 bola preta, enquanto a caixa II ficou com 3 bolas brancas e 3 bolas pretas. Em seguida, uma caixa foi escolhida e dela foi sorteada uma bola. Sabendo que a cor da bola sorteada era branca, a probabilidade de ter vindo da caixa I é de 3/8.
- C. Certo
- E. Errado
Considerando a matriz de transição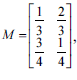 
, julgue os próximos itens acerca de cadeias de Markov.
A matriz de probabilidades de transição no segundo passo é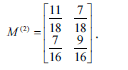 
- C. Certo
- E. Errado
Considerando os conceitos associados a probabilidade e estatística, julgue os itens de 108 a 116. A probabilidade de se obter um número menor que 5 no lançamento de um dado, sabendo que o dado não é defeituoso e que o resultado é um número ímpar, é igual a 2/3 .
- C. Certo
- E. Errado
Todo processo de Markov com dois estados é duplamente estocástico.
- C. Certo
- E. Errado
O processo não possui limite estacionário se p =1 e q =1.
- C. Certo
- E. Errado
Considerando os conceitos associados a probabilidade e estatística, julgue os itens de 108 a 116. A hipótese nula (H0) é a afirmação feita acerca do valor de um parâmetro populacional e o erro tipo I ocorre quando a hipótese nula é falsa e não é rejeitada.
- C. Certo
- E. Errado
O passeio aleatório simples não é uma cadeia de Markov.
- C. Certo
- E. Errado
No passo 1 (n =1), o passeio aleatório pode assumir valor -1 ou 1. Logo, nos passos pares 2n, esse processo assume valor par (inclusive o valor zero) com probabilidade 1; nos passos ímpares 2n + 1, esse mesmo processo assume valor ímpar com probabilidade 1.
- C. Certo
- E. Errado
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
