Questões sobre Probabilidade

Para orientar os investimentos em educação em certo município, um analista foi contratado para criar um ranking das escolas públicas desse município. Para cada escola, as variáveis disponíveis são a quantidade de turmas, a quantidade de alunos, a quantidade de professores, a nota da Prova Brasil e a área do terreno.

A partir dessa situação, julgue os itens subsequentes.

Considere que as áreas de todas as escolas desse município sejam distintas e que cada escola tenha obtido uma nota diferente na prova Brasil. Nessa situação, os modelos de probabilidade para variáveis aleatórias discretas são adequados para representar a distribuição de todas as variáveis analisadas por esse analista.

• C. Certo
• E. Errado

Julgue os próximos itens, considerando que o vetor aleatório (X, Y) possui distribuição conjunta de probabilidade conforme o quadro acima.

As variáveis aleatórias Z = X + Y e W = X -Y são dependentes.

• C. Certo
• E. Errado

Com respeito a distribuições conjuntas (X,Y), julgue os itens de 117 a 120.

• C. Certo
• E. Errado

Com respeito a distribuições conjuntas (X,Y), julgue os itens de 117 a 120.

• C. Certo
• E. Errado

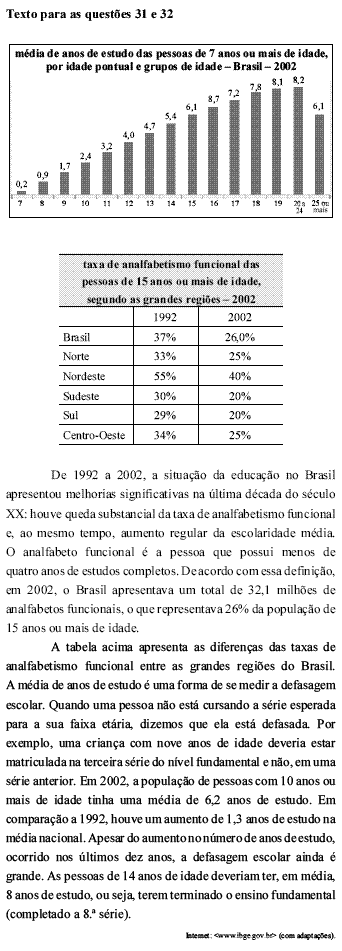
Uma pessoa com 15 anos de idade ou mais será selecionada ao acaso de cada região do país. Considerando-se as taxas de 2002, a probabilidade de haver uma única pessoa analfabeta funcional nessa amostra de 5 pessoas será

• A.

  inferior a 0,25.

• B.

  superior a 0,25 e inferior a 0,50.

• C.

  superior a 0,50 e inferior a 0,75.

• D.

  superior a 0,75.

Com base em amostragens históricas, aplicáveis a modelos de longo prazo que cobrem previsões em um horizonte temporal grande, os analistas inferem distribuições que possibilitam uma generalização maior sobre os dados. Em relação a variáveis aleatórias e distribuições de probabilidade, julgue os itens a seguir. A estimação se refere a inferências sobre os parâmetros de um modelo estocástico para os dados. A predição diz respeito a evidências não observadas.

• C. Certo
• E. Errado

Considere que uma empresa esteja negociando acordos comerciais com os parceiros potenciais A e B, e que P seja uma probabilidade tal que P(X = 1) = P(Y = 1) = 0,7 e P(X + Y = 0) = 0,3, em que as variáveis aleatórias X e Y estão assim definidas:

X = 1, se a negociação for bem sucedida junto a A;

X = 0, se a negociação não for bem sucedida junto a A;

Y = 1, se a negociação for bem sucedida junto a B;

Y = 0, se a negociação não for bem sucedida junto a B.

 Com base nessas informações, julgue os itens a seguir.

A probabilidade P(X + Y = 2) é igual ou inferior a 0,65.

• C. Certo
• E. Errado

Considere que uma empresa esteja negociando acordos comerciais com os parceiros potenciais A e B, e que P seja uma probabilidade tal que P(X = 1) = P(Y = 1) = 0,7 e P(X + Y = 0) = 0,3, em que as variáveis aleatórias X e Y estão assim definidas:

X = 1, se a negociação for bem sucedida junto a A;

X = 0, se a negociação não for bem sucedida junto a A;

Y = 1, se a negociação for bem sucedida junto a B;

Y = 0, se a negociação não for bem sucedida junto a B.

 Com base nessas informações, julgue os itens a seguir.

A variável aleatória X + Y segue uma distribuição binomial com parâmetros n = 2 e p = 0,7.

• C. Certo
• E. Errado

Considere que uma empresa esteja negociando acordos comerciais com os parceiros potenciais A e B, e que P seja uma probabilidade tal que P(X = 1) = P(Y = 1) = 0,7 e P(X + Y = 0) = 0,3, em que as variáveis aleatórias X e Y estão assim definidas:

X = 1, se a negociação for bem sucedida junto a A;

X = 0, se a negociação não for bem sucedida junto a A;

Y = 1, se a negociação for bem sucedida junto a B;

Y = 0, se a negociação não for bem sucedida junto a B.

 Com base nessas informações, julgue os itens a seguir.

A co-variância entre X e Y é superior a 0,20 e inferior a 0,25.

• C. Certo
• E. Errado

Em um julgamento, após ouvidas as testemunhas de defesa e de acusação, as considerações do promotor e do advogado de defesa, os jurados decidem pela culpabilidade ou não do réu. Cada jurado escreve em uma cédula "culpado" ou "inocente", e a votação, que é secreta, acontece uma única vez. Nesse caso, pode-se identificar cada voto como um experimento binomial em que "sucesso" significa "culpado" e que a probabilidade de sucesso para cada membro do júri é igual à do réu ser considerado culpado. Se existem N jurados, se a probabilidade do réu ser considerado culpado é S, então a probabilidade de exatamente T dos jurados votarem pela culpabilidade do réu é expressa pela função

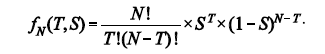
Com base nessas informações, julgue os itens a seguir.

Se S = 0,5 e N = 2, então a probabilidade de exatamente um dos jurados votar pela culpabilidade do réu é igual a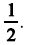

• C. Certo
• E. Errado