Questões sobre Probabilidade

Assinale a opção correta.

O benefício que pagará R$ 1.000,00, no final de cada mês, para a pessoa de 30 anos que atingir os 65 anos, com prêmio (ou contribuição) fracionado no início de cada mês, de forma imediata e durante o período de diferimento do benefício, pelo método prospectiva e antes de atingir a idade de direito ao benefício, terá a formulação da reserva matemática, segundo a metodologia de Woolhouse (tanto para o benefício quanto para o prêmio), dada por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja X uma variável aleatória discreta com função de probabilidade binomial f(x), onde f(x)= C_n,x p^x(1-p)^n-x e C_n,x é o número de combinações de n elementos tomados x a x. Sendo n=6 e p=1/3, determine f(6).

• A.

  1/729.

• B.

  1.

• C.

  0.

• D.

  64/729.

• E.

  8/729.

Um estudo para a estimação do número total, N, de usuários de drogas injetáveis foi realizado em um município no ano de 2006. A coleta de dados foi efetuada em duas fases por entrevistas face a face. A primeira fase (captura), que foi realizada nos meses de abril e maio de 2006, contou com n usuários entrevistados. A segunda fase (recaptura) foi realizada nos meses de agosto e setembro de 2006, com m usuários entrevistados. Com base nessas informações, considerando-se que N seja constante no período em questão e que todos os elementos da população tenham as mesmas chances de serem observados, julgue os itens subseqüentes.

Considerando-se que a amostragem na segunda fase seja aleatória simples sem reposição e que m = 2n, então a probabilidade de que metade da amostra seja formada por unidades recapturadas é igual a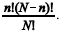

• C. Certo
• E. Errado

Sendo F(x) a função de distribuição da variável aleatória definida na questão anterior, determine F(0).

• A.

  0.

• B.

  1/729.

• C.

  64/729.

• D.

  243/729.

• E.

  1.

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

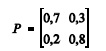
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

A probabilidade de transição do estado 0 no mês t para o estado 1 no mês t + 2 é inferior a 0,50.

• C. Certo
• E. Errado

Seja X a soma de n variáveis aleatórias independentes de Bernoulli, isto é, que assumem apenas os valores 1 e 0 com probabilidades p e 1-p, respectivamente. Assim, a distribuição de X é:

• A.

  Binomial com parâmetros n e p.

• B.

  Gama com parâmetros n e p.

• C.

  Qui quadrado com n graus de liberdade.

• D.

  Laplace.

• E.

  "t" de Student com n-1 graus de liberdade.

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

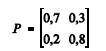
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

Dado que, nos meses t - 1 e t, Roberto fez a opção por medicamentos genéricos, a probabilidade de ele optar novamente pelo genérico no mês t + 1 é superior a 0,5.

• C. Certo
• E. Errado

Uma população de indivíduos é constituída 80% por um tipo genético A e 20% por uma variação genética B. A probabilidade de um indivíduo do tipo A ter determinada doença é de 5%, enquanto a probabilidade de um indivíduo com a variação B ter a doença é de 40%. Dado que um indivíduo tem a doença, qual a probabilidade de ele ser da variação genética B?

• A.

  1/3.

• B.

  0,4.

• C.

  0,5

• D.

  0,6.

• E.

  2/3.

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

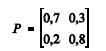
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

No limite estacionário, a probabilidade de Roberto adquirir um medicamento genérico é igual à probabilidade de Roberto adquirir um medicamento não genérico.

• C. Certo
• E. Errado

A probabilidade de qualquer um deles ser contratado é 1/2

• C. Certo
• E. Errado