Questões sobre Probabilidade

Considere que X(t) represente o número de postos de trabalho disponíveis no instante t e que Y(t) represente o número de trabalhadores disponíveis no instante t para a ocupação desses postos. Considere também que X(t) e Y(t) sejam independentes e sigam processos estocásticos de Poisson. Nesse modelo, os valores esperados de X(t) e Y(t) são, respectivamente, iguais a 5t e 6t, em que t é um número real não-negativo, e o excesso de trabalhadores em relação à quantidade de postos disponíveis é definido pela diferença D(t) = Y(t) - X(t). Com base nessas definições, julgue os itens a seguir.

Se Y(50) = 100, então Y(49) > 100.

• C. Certo
• E. Errado

Considere que Z seja uma variável aleatória normal padrão e que Y seja uma variável aleatória de Bernoulli com parâmetro p = 0,9. Considere também que a esperança condicional de Z para Y = 1 seja igual  a 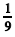 . Nessa situação, julgue os itens a seguir.

A esperança condicional de Z dado que Y = 0 é superior a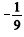

• C. Certo
• E. Errado

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 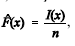 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

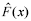é um estimador não-viciado (ou não-tendencioso) para F(x).

• C. Certo
• E. Errado

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 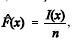 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

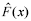é um estimador consistente para F(x).

• C. Certo
• E. Errado

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 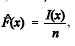 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

Para cada valor real x, a distribuição amostral de é 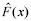assintoticamente normal.

• C. Certo
• E. Errado

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 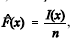 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

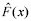 é um estimador de máxima verossimilhança para F(x).

• C. Certo
• E. Errado

O coeficiente de variação amostral (em porcentagem) de um conjunto de salários é 110%. Se os salários desse conjunto forem reajustados em 20%, o novo coeficiente de variação amostral será:

• A.

  110%.

• B.

  112,2%.

• C.

  114,2%.

• D.

  122%.

• E.

  130%.

Considerando um vetor aleatório (X, Y) distribuído na função de densidade conjunta 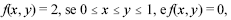caso contrário, julgue os itens a seguir.

A probabilidade P(X + Y < 0,5) é inferior a 0,15.

• C. Certo
• E. Errado

A tabela a seguir apresenta o número estimado da população em cada região brasileira no ano de 2007 (fonte: IBGE), a porcentagem estimada de pessoas por região que possuem aparelho de telefone celular (fonte: TIC Domicílios do NIC.br), e a multiplicação dessas duas quantidades por região (pop x cel), com duas casas decimais de precisão:

De acordo com a tabela acima, a probabilidade aproximada de um brasileiro que possui aparelho celular viver na região Norte ou na região Sul é:

• A.

  12,4%.

• B.

  20,2%.

• C.

  24,1%.

• D.

  35,8%.

• E.

  42,6%.

Considere que X₁, X₂, ..., X_n seja uma amostra aleatória simples de uma distribuição X, cuja função de densidade é dada por para para x < 0 ou x > 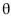 em que  > 0. Com base nessas informações, julgue os itens a seguir. Realizações de X podem ser obtidas por meio de 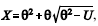 em que U é uma distribuição uniforme no intervalo [0, ].

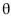• C. Certo
• E. Errado