Questões sobre Séries Temporais

O seguinte modelo foi ajustado a uma série temporal de produção de certo produto:

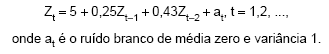
O modelo ajustado

• A.

  é um modelo de médias móveis de ordem dois.

• B. é um modelo estacionário, mas com tendência linear.
• C.

  tem média 5.

• D.

  é um modelo autorregressivo de ordem dois.

• E.

  não é invertível.

Seja {X_t, t ∈ Z} um processo estocástico onde as variáveis X_t são não correlacionadas, isto é, Cov {X_t, Xs} = 0, t ≠ s e Z é o conjunto dos números inteiros. O processo X_t é um

• A.

  passeio aleatório discreto.

• B.

  movimento browniano.

• C.

  ruído branco discreto.

• D.

  processo de Markov.

• E.

  processo puramente aleatório.

Um gráfico de controle de um processo produtivo indica que o processo está sob controle se o conjunto de pontos do gráfico

• A.

  tiver todos os pontos situados entre a linha central e o limite superior de controle do gráfico.

• B.

  apresentar tendência linear.

• C.

  apresentar sazonalidade estocástica.

• D.

  apresentar variabilidade crescente ao redor da linha central.

• E.

  tiver todos os pontos situados dentro dos limites de controle, tendo um comportamento estacionário.

Considere o modelo autorregressivo de ordem dois AR(2) dado por:

Z_t = φ₁Z_t−₁ + φ2Z_t−2 + a_t

Onde t a é o ruído branco de média zero e variância 2a σ^_a2 . Se Z_t é estacionário, então o valor da função de autocorrelação no lag 1 é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Sejam f(k), k = 1,2,3,... e g(k), k = 1,2.3,... as funções de autocorrelação (fac) e autocorrelação parcial (facp), respectivamente, de um modelo ARMA(p,q). Considere as seguintes afirmações:

I. Para um ARMA(1,0), f(k) só difere de zero para k = 1 e g(k) decai exponencialmente.

II. Para um ARMA(1,1), f(k) só difere de zero para k = 1 e g(k) decai exponencialmente.

III. Para um ARMA(0,2), f(k) só difere de zero para k = 1 e k = 2 e g(k) é dominada por misturas de exponenciais ou senoides amortecidas.

IV. Para um ARMA(2,0), f(k) é dominada por misturas de exponenciais ou senoides amortecidas e g(k) = 0, somente para k = 1 e para k > 1 decai exponencialmente.

Está correto o que se afirma SOMENTE em

• A.

  I e III.

• B.

  III e IV.

• C.

  I, II e III.

• D.

  III.

• E.

  I.

Considere o modelo ARIMA(0,0,2) dado por

X_t = θ₀ + a_t − θ₁a_t−1 + θ₂a_t−2 ,

onde at é o ruído branco de média zero e variância σ² , e θ0 é uma constante. É correto:

• A.

  X_t só é estacionário se

• B.

  X_t é um processo sempre invertível.

• C.

  X_t só  estacionário se  for zero.

• D.

  X_t é sempre estacionário.

• E.

  X_t só é invertível se

Considere as afirmativas abaixo relativamente a séries temporais.

É correto o que se afirma APENAS em

• A.

  I.

• B.

  I e II.

• C.

  II, III e IV.

• D.

  II e IV.

• E.

  I e IV.

Considere o modelo autorregressivo de ordem dois AR(2) dado por:

Zt = φ1Zt−1 + φ2Zt−2 + at

onde t a é o ruído branco de média zero e variância 2a σ .

Considere as seguintes condições: I. φ1 + φ2 < 1 II. −1< φ1 + φ2 < 1 III. −1< φ2 <1 IV. φ2 − φ1 <1 V. −1< φ1 <1

O processo Zt é estacionário APENAS se satisfaz às condições

• A.

  I, II e III.

• B.

  I, II e V.

• C.

  I, III e IV.

• D.

  I, IV e V.

• E.

  II, III e IV.

Considere as seguintes afirmações:

I. Para um processo ARMA (1, 1) a função de autocorrelação parcial só é diferente de zero no lag 1.

II. Para um processo ARMA (1, 1), onde φ é o coeficiente autoregressivo e θ é o coeficiente de médias móveis, a região de admissibilidade é dada por |φ| < 1 e |θ| < 1.

III. De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em componentes senoidais com coeficientes aleatórios não-correlacionados.

IV. Um processo ARIMA (1, d ,1), onde d = 1, é estacionário.

Está correto o que se afirma APENAS em

• A.

  I e II.

• B.

  I, II e III.

• C.

  I e III.

• D.

  II e III.

• E.

  II e IV.

Texto para as questões de 26 a 29

A figura acima apresenta a evolução temporal da quantidade de carvão vegetal - em toneladas - produzida no Brasil entre os anos 1990 e 2006. Ao longo desse período, a produção anual média de carvão vegetal foi de 2,4 milhões de toneladas/ano, o desvio padrão amostral foi de 470 mil toneladas e a correlação linear entre a produção e o ano foi igual a 0,15.

Quanto à utilização das técnicas de análise de séries temporais nos dados apresentados no texto,

• A.

  a evolução temporal da quantidade de carvão vegetal - em toneladas - produzida no Brasil entre os anos 1990 e 2006 é uma série sazonal.

• B.

  o método de alisamento de Holt-Winters pode ser aplicado para gerar previsões para séries temporais com tendência de crescimento linear.

• C.

  o filtro de Kalman é um algoritmo para o cálculo de previsões, mas a sua utilização não é recomendada para séries não estacionárias.

• D.

  o algoritmo de Durbin-Levinson é um algoritmo não recursivo para o cálculo de previsões de máxima verossimilhança tanto para as séries temporais estacionárias como para as que não são estacionárias.