Questões sobre Séries Temporais

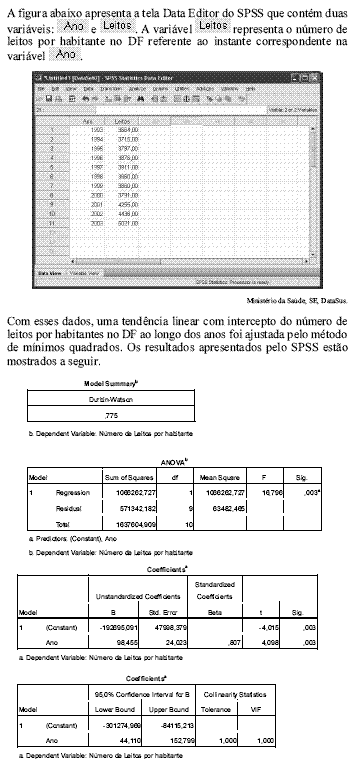
Tendo como referência essas informações, julgue os itens de 64 a 76.

A seqüência do número de leitos ao longo do tempo forma uma série temporal fracamente estacionária.

• C. Certo
• E. Errado

A série histórica da quantidade mensal de autorizações de procedimentos de alta complexidade em oncologia, em determinado município, no período de novembro de 1998 a fevereiro de 2003, foi descrita por dois pesquisadores por meio de um modelo ARIMA(3,1,0). Considerando que Z _t representa a quantidade de autorizações de procedimentos de alta complexidade em oncologia nesse município no mês _t, e que o modelo ARIMA(3,1,0) apresentado foi aquele que produz o menor AIC (Akaike's information criterion), julgue os itens subseqüentes.

A série histórica {Z_t} não é estacionária.

• C. Certo
• E. Errado

A série histórica da quantidade mensal de autorizações de procedimentos de alta complexidade em oncologia, em determinado município, no período de novembro de 1998 a fevereiro de 2003, foi descrita por dois pesquisadores por meio de um modelo ARIMA(3,1,0). Considerando que Z _t representa a quantidade de autorizações de procedimentos de alta complexidade em oncologia nesse município no mês _t, e que o modelo ARIMA(3,1,0) apresentado foi aquele que produz o menor AIC (Akaike's information criterion), julgue os itens subseqüentes.

Se o modelo estiver correto, a autocorrelação entre Z _t e Z _{t + k} será nula se |k| > 3.

• C. Certo
• E. Errado

A série histórica da quantidade mensal de autorizações de procedimentos de alta complexidade em oncologia, em determinado município, no período de novembro de 1998 a fevereiro de 2003, foi descrita por dois pesquisadores por meio de um modelo ARIMA(3,1,0). Considerando que Z _t representa a quantidade de autorizações de procedimentos de alta complexidade em oncologia nesse município no mês _t, e que o modelo ARIMA(3,1,0) apresentado foi aquele que produz o menor AIC (Akaike's information criterion), julgue os itens subseqüentes.

O ajuste produzido pelo modelo ARIMA (3,1,0) é equivalente ao alisamento exponencial triplo.

• C. Certo
• E. Errado

A série histórica da quantidade mensal de autorizações de procedimentos de alta complexidade em oncologia, em determinado município, no período de novembro de 1998 a fevereiro de 2003, foi descrita por dois pesquisadores por meio de um modelo ARIMA(3,1,0). Considerando que Z _t representa a quantidade de autorizações de procedimentos de alta complexidade em oncologia nesse município no mês _t, e que o modelo ARIMA(3,1,0) apresentado foi aquele que produz o menor AIC (Akaike's information criterion), julgue os itens subseqüentes.

Considere que os dois primeiros coeficientes autoregressivos do modelo ajustado sejam nulos e que o terceiro seja positivo. Nessa situação, a série histórica é sazonal.

• C. Certo
• E. Errado

A série histórica da quantidade mensal de autorizações de procedimentos de alta complexidade em oncologia, em determinado município, no período de novembro de 1998 a fevereiro de 2003, foi descrita por dois pesquisadores por meio de um modelo ARIMA(3,1,0). Considerando que Z _t representa a quantidade de autorizações de procedimentos de alta complexidade em oncologia nesse município no mês _t, e que o modelo ARIMA(3,1,0) apresentado foi aquele que produz o menor AIC (Akaike's information criterion), julgue os itens subseqüentes.

A autocorrelação parcial entre Z _t - Z _t-1 e (Z _{t + k} - Z _{t + k-1} será nula se |k| < 4.

• C. Certo
• E. Errado

Um estatístico analisou a série histórica do total anual de óbitos em certo município, de 1980 a 1999, e representou essa série temporal por {X(t)}, em que t = 1, 2, 3, ..., 20 correspondem, respectivamente, aos anos 1980, 1981, 1982, ..., 1999. A tabela acima apresenta parte da função de autocorrelação amostral e da função de autocorrelação parcial amostral. Com base nessas informações, julgue os itens de 76 a 81.

• C. Certo
• E. Errado

Um estatístico analisou a série histórica do total anual de óbitos em certo município, de 1980 a 1999, e representou essa série temporal por {X(t)}, em que t = 1, 2, 3, ..., 20 correspondem, respectivamente, aos anos 1980, 1981, 1982, ..., 1999. A tabela acima apresenta parte da função de autocorrelação amostral e da função de autocorrelação parcial amostral. Com base nessas informações, julgue os itens de 76 a 81.

O valor da autocorrelação parcial na defasagem 5 não é estatisticamente significativo ao nível de 5%.

• C. Certo
• E. Errado

Um estatístico analisou a série histórica do total anual de óbitos em certo município, de 1980 a 1999, e representou essa série temporal por {X(t)}, em que t = 1, 2, 3, ..., 20 correspondem, respectivamente, aos anos 1980, 1981, 1982, ..., 1999. A tabela acima apresenta parte da função de autocorrelação amostral e da função de autocorrelação parcial amostral. Com base nessas informações, julgue os itens de 76 a 81.

A autocorrelação parcial amostral pode ser obtida com a ajuda do algoritmo de Durbin-Levinson.

• C. Certo
• E. Errado

A série temporal {X(t)} é estacionária.

• C. Certo
• E. Errado