Questões sobre Séries Temporais

Considerando que uma série temporal {Z_t}_{t = 1,..., n,} em que Zt representa o número mensal de ligações recebidas por uma central de atendimento ao cliente no mês t, segue um processo SARIMA(0,1,1) × (0,1,1)₁₂, julgue os itens subsequentes.

A série temporal {Z_t}_{t = 1,..., n} é estacionária.

• C. Certo
• E. Errado

Considerando que uma série temporal {Z_t}_{t = 1,..., n,} em que Zt representa o número mensal de ligações recebidas por uma central de atendimento ao cliente no mês t, segue um processo SARIMA(0,1,1) × (0,1,1)₁₂, julgue os itens subsequentes.

• C. Certo
• E. Errado

Considerando que uma série temporal {Z_t}_{t = 1,..., n,} em que Zt representa o número mensal de ligações recebidas por uma central de atendimento ao cliente no mês t, segue um processo SARIMA(0,1,1) × (0,1,1)₁₂, julgue os itens subsequentes.

A série temporal {Zt}_{t = 1,..., n} possui sazonalidade estocástica de período anual.

• C. Certo
• E. Errado

O modelo clássico para séries temporais supõe que a série temporal Zt, t=1, 2, . . . , N pode ser escrita como Zt = Tt + St + at , t=1, 2, . . . , N, ou seja, segundo uma soma de três componentes: uma tendência, uma componente sazonal e um termo aleatório. Com relação ao modelo considerado podemos afirmar que:

• A.

  ele é aditivo, sendo adequado, por exemplo, quando St depende das outras componentes;

• B.

  a componente sazonal aparece quando as observações são anuais, isto é, registradas anualmente;

• C.

  a tendência em séries econômicas ou demográficas é causada por fatores que são medidos durante curtos períodos de tempo;

• D.

  quando representamos f(t) = Tt + St por alguma função suave do tempo, então f(t) é encarada como uma função determinística do tempo.

Considere um processo estacionário. A facv (função de autocovariância)  definida por satisfaz às seguintes propriedades:

• A.

  

• B.

  

• C.

  

• D.

  

Quanto às séries histórica (ou temporal) e geográfica é incorreto afirmar que:

• A. A série histórica (ou temporal) é constituída pelo registro de uma série de observações em ocasiões distintas.
• B. Uma série geográfica é constituída pelo registro de uma seqüência de observações colhidas em um mesmo lugar.
• C. Na série histórica, o período das observações varia, mantendo-se fixos o lugar e o tipo de observação.
• D. Na série geográfica, variam os lugares geográficos das observações e são mantidos fixos o tempo e a categoria.
• E. Observações sobre a variação da temperatura média diária em uma cidade podem gerar uma série histórica.

Considerando que uma série temporal {Z _t}, em que  t = 1, ..., n, e Z_t representa o número de processos judiciais julgados por um tribunal no mês t, segue um processo SARIMA(0, 0, 0) × (0, 0, 1)₁₂ com uma constante, julgue os itens subsequentes.

A série temporal {Z _t}, t = 1, ..., n, é estacionária.

• C. Certo
• E. Errado

Considerando que uma série temporal {Z _t}, em que  t = 1, ..., n, e Z_t representa o número de processos judiciais julgados por um tribunal no mês t, segue um processo SARIMA(0, 0, 0) × (0, 0, 1)₁₂ com uma constante, julgue os itens subsequentes.

O modelo SARIMA(0, 0, 0) × (0, 0, 1)₁₂ com uma constante  tem a forma (1 - D ¹²)Z_t 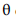= (1 - D)(1- D¹² )a_t , em que D  é o operador de atraso, 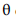e são os coeficientes da parte de médias móveis do modelo e a_t representa o ruído branco.

• C. Certo
• E. Errado

Considerando que uma série temporal {Z _t}, em que  t = 1, ..., n, e Z_t representa o número de processos judiciais julgados por um tribunal no mês t, segue um processo SARIMA(0, 0, 0) × (0, 0, 1)₁₂ com uma constante, julgue os itens subsequentes.

A autocorrelação entre Z_t e Z_{t +h} , em que 1  h  11, é igual a zero.

• C. Certo
• E. Errado

Considerando que uma série temporal {Z _t}, em que  t = 1, ..., n, e Z_t representa o número de processos judiciais julgados por um tribunal no mês t, segue um processo SARIMA(0, 0, 0) × (0, 0, 1)₁₂ com uma constante, julgue os itens subsequentes.

A autocorrelação parcial entre Z_t+3 e Z_t+6 é igual a zero.

• C. Certo
• E. Errado