Questões sobre Variância / Variância Amostral / Variância Absoluta

Seja a variável aleatória Y = 2X1 − X2 + 3X3 , a variância de Y é igual a

• A.

  20.

• B.

  15.

• C.

  24.

• D.

  13.

• E.

  21.

A variância da estimativa da média foi inferior a 1.000.

• C. Certo
• E. Errado

Acerca da Análise Multivariada, considere:

I. Na análise fatorial, o critério varimax é um método de rotação fatorial ortogonal para se conseguir uma estrutura fatorial simplificada.

II. O princípio subjacente da análise de correlação canônica é desenvolver uma combinação linear de cada conjunto de variáveis, dependentes e independentes, visando minimizar a correlação entre os dois conjuntos.

III. A análise de correspondência acomoda tanto dados não métricos quanto relações não lineares.

IV. A análise discriminante é apropriada quando a variável dependente é categórica e as variáveis independentes são métricas.

Está correto o que consta APENAS em

• A.

  I e IV.

• B.

  II e III.

• C.

  I, II e III.

• D.

  II e IV.

• E.

  I, III e IV.

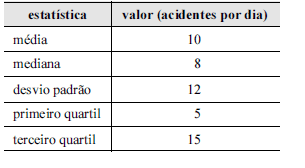
A tabela acima apresenta as estatísticas produzidas em um levantamento acerca do número diário de acidentes que envolvem motocicletas em determinado local. Com base nessas informações, julgue os próximos itens.

A variância da distribuição do número diário de acidentes com motocicletas no referido local é inferior a 100.

• C. Certo
• E. Errado

Uma variável aleatória contínua X tem média 20 e, pelo Teorema de Tchebichev, a probabilidade mínima de que pertença ao intervalo (19, 21) é igual a 84%. A variância de X é igual a

• A. 0,16.
• B. 0,25.
• C. 0,40.
• D. 1,00.
• E. 0,64.

Considere que E = (m−1)X − mY + 2Z corresponde a uma classe de estimadores não viesados da média μ de uma população normalmente distribuída com variância σ² ≠ 0. (X, Y, Z) é uma amostra aleatória, com reposição, desta população com m sendo um parâmetro real. O estimador mais eficiente desta classe apresenta uma variância igual a

• A. 2,5 σ².
• B. 3,0 σ².
• C. 4,5 σ².
• D. 5,0 σ².
• E. 6,0 σ².

• A. 15,300.
• B. 16,150.
• C. 17,100.
• D. 18,165.
• E. 19,380.

Em 3 empresas (X, Y e Z) foram escolhidos por sorteio, em cada uma, 12 operários para realização de um treinamento. Após o treinamento, foi realizado um teste, independentemente, com todos estes 36 operários e deseja-se saber, ao nível de significância de 5%, se as médias das respectivas notas dos grupos formados por cada empresa são iguais. Pelo quadro de análise de variância, verificou-se que a soma de quadrados referente à fonte de variação entre grupos representou 47,2% da fonte de variação total. O valor da estatística F (F calculado) utilizado para comparar com o F tabelado (distribuição F de Snedecor), com o objetivo de verificação da igualdade das médias, é

• A. 12,50.
• B. 12,25.
• C. 13,50.
• D. 14,75.
• E. 15,00.

A probabilidade de que um evento resulte em sucesso é p. Seja X a variável aleatória que representa o número de repetições independentes do evento até que ocorram dois sucessos. Sabendo-se que a probabilidade de X ser igual a 4 é igual à probabilidade de X ser igual a 5, a variância de X é igual a

• A. 22,0.
• B. 26,0.
• C. 20,0.
• D. 24,0.
• E. 21,0.

Uma cidade tem 12.000 domicílios divididos em três bairros (denotados por B1, B2 e B3), que pagam IPTU em três faixas de valores (denotadas por I1, I2 e I3). Sabe-se que um pesquisador deseja estimar a média da renda mensal destes domicílios via Amostragem Estraficada ou Amostragem por Conglomerados de 1.200 domicílios. O quadro a seguir mostra o número de domicílios e a variância da renda mensal em cada faixa de IPTU e em cada bairro. A variância da renda mensal entre todos os domicílios da região é igual a 3.400 (variância global).

Com o objetivo de aumentar a precisão do estimador da média da renda mensal, é correto afirmar que

• A. a variável “bairro” é a mais adequada para formação de estratos, pois os três bairros têm número de domicílios iguais.
• B. a variável “bairro” é a mais adequada para formação de conglomerados, pois os três bairros têm número de domicílios iguais.
• C. a variável “IPTU” é a mais adequada para formação de estratos, pois suas três faixas têm número de domicílios diferentes.
• D. a variável “bairro” é a mais adequada para formação de estratos, pois a variabilidade da renda domiciliar dentro de cada bairro é próxima da variabilidade global.
• E. a variável “IPTU” é a mais adequada para formação de estratos, pois a variabilidade da renda domiciliar dentro de cada faixa de IPTU é menor do que a variabilidade global.