Questões de Estatística da Fundação Carlos Chagas (FCC)

Considere uma amostra aleatória de tamanho 4: (X, Y, Z, T) extraída de uma população normal de média μ e variância unitária. A classe de estimadores E = (K − 2) X − KY + (2 − K) Z + (K + 1) T é utilizada para estimar a média μ da população, sendo K um parâmetro real. Entre os estimadores desta classe, o mais eficiente apresenta uma variância igual a

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Um estudo corresponde ao interesse de analisar o desempenho de 3 postos independentes de atendimento ao público com 8 funcionários cada um. Decidiu-se empregar a análise de variância com o objetivo de testar a hipótese de igualdade das médias de atendimento dos 3 postos (quantidade de pessoas atendidas por mês). Durante um mês, anotou-se para cada funcionário dos postos a quantidade de pessoas atendidas. Denominando os postos por Grupo 1, Grupo 2 e Grupo 3 obteve-se pelo quadro de análise de variância o valor da estatística F_c (F calculado) igual a 2, para posteriormente comparar com o F tabelado (variável F de Snedecor). A porcentagem que a “variação entre os grupos” representa da “variação total” no quadro de análise de variância é igual a

• A.

  8%.

• B.

  12%.

• C.

  16%.

• D.

  24%.

• E.

  32%.

Um analista de mercados está coletando informações sobre a variável X = preço de determinado produto. Ele coletou uma amostra aleatória, sem reposição, de tamanho n de uma população de 45 compradores do produto. Sabendo-se que a variância da média amostral ( X ) dos preços pagos pelos n clientes pelo produto é 1/11 da variância populacional (variância de X para a população finita de 45 compradores), o valor de n é

• A.

  10.

• B.

  9.

• C.

  8.

• D.

  6.

• E.

  5.

A variância da variável aleatória Z = X + Y é dada por

• A.

  1/9

• B.

  2/9

• C.

  1/3

• D.

  4/9

• E.

  2/3

Em uma distribuição de valores determinando uma curva de frequência unimodal, verificou-se que o valor da mediana é superior

I. A curva possui a cauda mais alongada à direita.

II. A distribuição é assimétrica à direita.

III. A amplitude do intervalo entre a moda e a mediana é inferior à amplitude do intervalo entre a mediana e a média.

IV. Os valores da distribuição estão fortemente concentrados em torno da mediana.

V. Metade dos valores da distribuição situam-se entre o valor da moda e o valor da média.

• A.

  1.

• B.

  2.

• C.

  3.

• D.

  4.

• E.

  5.

Um estudo apresentou em seu relatório um problema de programação linear que é descrito abaixo.

Minimizar: Z = 10 x + 25 y

Sujeito a: 2 x + y ≥ 5

               x + 2y ≥ 7

               x + 3 y ≥ 9

               x ≥ 0 e y ≥ 0

Os valores de x e y são, respectivamente,

• A.

  3,0 e 2,0.

• B.

  1,0 e 3,0.

• C.

  1,2 e 2,6.

• D.

  1,0 e 2,5.

• E.

  2,0 e 3,0.

Considere as afirmativas abaixo.

I. A taxa de mortalidade infantil é definida como o número de mortes durante um ano-calendário entre os bebês com menos de um ano de idade dividido pelo número total de nascidos vivos durante aquele ano.

II. O sexo e a raça dos indivíduos em uma população não têm efeito significativo nas taxas que descrevem as estatísticas vitais.

III. Dados demográficos lidam exclusivamente com o crescimento de uma população.

Está correto o que se afirma APENAS em

• A.

  I.

• B.

  II.

• C.

  III.

• D.

  I e II.

• E.

  I e III.

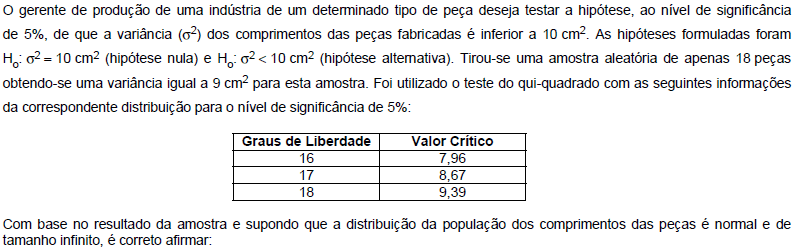
• A.

  ao nível de significância de 5%, a variância é inferior a 10 cm².

• B.

  o valor do qui-quadrado observado para comparação com o qui-quadrado tabelado é superior a 8,67 e inferior a 9,39.

• C.

  para qualquer nível de significância, a conclusão é que a variância populacional é inferior a 10 cm².

• D.

  o número de graus de liberdade aplicado ao teste é igual a 16.

• E.

  para qualquer nível de significância inferior a 5% a conclusão é de que a variância dos comprimentos das peças não é inferior a 10 cm².

Seja uma população da qual se extrai uma amostra aleatória grande de tamanho n. Com relação à aplicação do método de reamostragem bootstrap, é correto afirmar que tal método

• A.

  computa n subconjuntos pela eliminação sequencial de um caso em cada amostra. Assim, cada amostra tem um tamanho (n−1) e difere apenas pelo caso omitido em cada amostra.

• B. obtém sua amostra via amostragem sem reposição da amostra original de tamanho n.
• C.

  exige que a distribuição da população seja normal.

• D.

  pode ser utilizado para encontrar o intervalo de confiança para um parâmetro analisado da população.

• E.

  desconsidera que a amostra original de tamanho n não representa toda a população.

Com base nessa função, é verdade que a função geratriz de momentos de uma variável aleatória exponencial com parâmetro α > 0, para t < α , é:

• A.

  

• B.

  

• C.

  

• D.

  

• E.