Questões de Matemática

Julgue os itens que se seguem, acerca da aplicação de razões e proporções e de equações.

Considere que, para construir um reservatório, 30 homens trabalharam durante 18 dias e, em seguida, 36 homens trabalharam durante 12 dias. Considerando ainda que os homens produzam a mesma quantidade de serviço por dia de trabalho, se 36 homens tivessem trabalhado ininterruptamente, é correto afirmar que a obra teria ficado pronta em menos de 25 dias.

• C. Certo
• E. Errado

Um problema clássico consiste em calcular valores de x de modo que 10^x tenha resultados iguais a 1, 2, 3, 4, 5, 6, etc, com boa aproximação.

O valor de x em 10^x=1 é x= 0, pois 10⁰ = 1

Para calcular o valor de x em 10^x = 2, adotaremos a seguinte estratégia: vamos escrever potências de 10 e potências de 2 e procurar, dentre elas, os valores mais próximos.

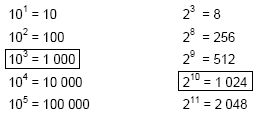
Aproximando 1000 para 1024, teremos:

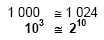
Extraíndo a raiz décima de ambos os membros, ficaremos com o seguinte:

Com base nesse procedimento e considerando a aproximação entre 2 x 10⁴ = 20 000 e 3⁹ = 19 683, o valor de x para 10^x = 3 é

• A.

  0,330

• B.

  0,410

• C.

  0,478

• D.

  0,555

• E.

  0,984

Simplificando a fração 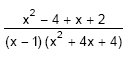 , na qual x ≠ 1 e x ≠ −2 obtém-se

• A.

  

• B.

  

• C.

  

• D.

  x - 1

• E.

  x + 2

Um juiz deve julgar 52 processos, que estão separados, por assunto, em 3 grupos. Sabe-se que o máximo divisor comum (MDC) e o mínimo múltiplo comum (MMC) entre os números de processos em cada um dos grupos são 4 e 48, respectivamente. Acerca desses grupos de processos, julgue os itens seguintes.

Um dos grupos contém 8 processos.

• C. Certo
• E. Errado

Analisando a grande diversidade de respostas que diferentes crianças podem produzir frente ao mesmo problema, Delia Lerner Zunino, em seu livro Matemática na escola: aqui e agora, coloca a questão: Como fazer para que a diversidade constitua-se em um fator positivo para o aprendizado?

Segundo a autora, os três elementos da resposta geral a essa pergunta são:

• A.

  cooperação entre as crianças, confrontação das diversas estratégias, validação das estratégias adotadas.

• B.

  repetição de processos detectados como corretos, análise de expectativas futuras, contextualização.

• C.

  verificação da resposta, confrontação de métodos utilizados, escolha do método considerado mais eficiente.

• D.

  estipulação de tempo dedicado à resolução, eleição do processo que tenha demandado tempo mais curto, aceitação da estratégia eleita como mais eficiente.

• E.

  listagem dos métodos de resolução disponíveis, análise dos métodos realmente utilizados, valorização dos métodos que permitiram acertos.

No conjunto dos números reais a inequação a x 0 x b ≥ − + tem por conjunto-solução { x∈ R / − 3 ≤ x < 4} . Os valores de a e b são, respectivamente,

• A.

  − 3 e − 4

• B.

  − 3 e 4

• C.

  3 e 4

• D.

  3 e − 4

• E.

  3 e − 3

Um certo helicóptero pode percorrer 150 km em 0,5 horas. Mantendo esta velocidade quantos quilômetros percorrerá em 2 horas?

• A.

  450 km.

• B.

  600 km.

• C.

  900 km.

• D.

  300 km.

Dois bairros de uma cidade são ligados por uma estrada reta medindo D km. Um motorista saiu de um desses bairros por essa estrada, percorreu x km até um posto de abastecimento localizado em um ponto intermediário entre os bairros e depois completou o percurso dirigindo por mais y km até o outro bairro. Julgue os itens seguintes, acerca desse percurso.

Se o posto de abastecimento divide a distância entre os dois bairros na proporção de 1 para 3 e xy = 75, então D é inferior a 25.

• C. Certo
• E. Errado

Vamos definir problemas de pesquisa aberta como sendo aqueles em cujo enunciado não há uma estratégia implícita para resolvê-los, nem operações imediatas. Demonstrações de teoremas enquadram-se nessa categoria, assim como questões do tipo "encontre todos...". Leia os problemas:

I. Quais são os números naturais que têm um número ímpar de fatores?

II. Quantos triângulos diferentes, de lados de medidas inteiras, podem ser construídos de modo que o lado maior tenha 5 cm de comprimento? 6 cm? n centímetros?

III. Uma bolsa com moedas de 5, 10 e 25 centavos contém 435 moedas no valor de R$ 43,45 . Há três vezes mais moedas de 10 do que de 25. Quantas moedas de cada tipo estão na bolsa?

IV. Imagine n armários, todos fechados, e n pessoas. Suponha que a primeira pessoa passe e abra todos os armários. Depois, passe uma segunda pessoa e feche um armário sim e o outro não, começando pelo número 2. A terceira pessoa, então, passa e altera o estados das portas dos armários, de três em três, começando pelo número 3 (isto é, se este está aberto, ela o fecha, e vice-versa). Se esse procedimento continuar até que todas as n pessoas passem, quais dentre as portas ficarão abertas?

Com respeito a esses problemas, é INCORRETO afirmar que

• A.

  o problema IV apresenta uma forma instigante de apresentar a mesma situação que aparece no problema I.

• B.

  o problema II é de pesquisa aberta porque propicia ao aluno a experiência de buscar e encontrar um padrão geométrico.

• C.

  o problema III já traz uma estratégia de resolução no enunciado. O obstáculo a vencer é apenas o de traduzir a palavra escrita pela forma matemática apropriada, de maneira a usar as equações adequadas.

• D.

  se reconhece o problema I como de pesquisa aberta pelo tipo de pergunta que faz.

• E.

  apenas o problema IV é de pesquisa aberta.

O gráfico da figura mostra as coordenadas do ponto máximo de uma função de segundo grau do tipo f(x) = ax2 + bx + c

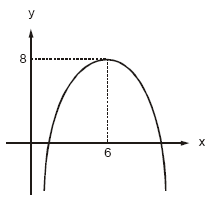
• A.

  4 < x < 6

• B.

  4 < x < 8

• C.

  6 − 2  < x < 6 + 2

• D.

  x < 4 ou x > 8

• E.

  x < 6 − 2  ou x > 6 + 2