Questões de Matemática

O professor de matemática determinou a seus alunos:

1) cada um pegue uma folha de papel, retangular, de lados medindo 20 cm × 16 cm; dobrem a folha ao meio, pelo lado de maior comprimento, identificando os seus lados opostos (como na figura abaixo);

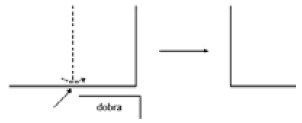
2) repitam esse processo com a folha dobrada (ilustrado na figura abaixo);

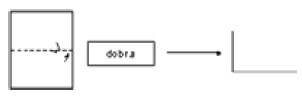
3) repitam o processo várias vezes.

Acerca dos resultados dessa atividade e considerando que seja possível repetir o processo indefinidamente, julgue os itens subseqüentes.

Ao abrir a folha de papel, depois de dobrá-la por 8 vezes, as marcas das dobras dividem a folha em 256 retângulos de mesma área.

• C. Certo
• E. Errado

Considere, em um sistema de coordenadas cartesianas ortogonais xOy, a região de área finita e limitada pelos gráficos das funções f(x) = x² e g(x) = 9. Se a reta y = K divide essa região em duas partes de áreas iguais, então K é tal que

• A.

  K³ = 27

• B.

  K^2/3 = 27/2

• C.

  K³ = 9/2

• D.

  K^3/2 = 9/4

• E.

  K³ = 27/16

Utilizando um programa computacional gráfico, um aluno do ensino médio desenhou, para alguns valores constantes k > 0, o gráfico da função exponencial y = k ax, em que a é uma constante. Esses gráficos estão ilustrados na figura abaixo.

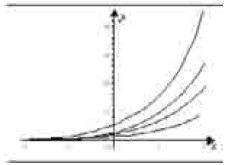
Com base nessas informações e na figura acima, julgue os itens a seguir.

Para cada valor de k o gráfico correspondente à função y = k ax intercepta o eixo Oy no ponto de coordenadas (0, k).

• C. Certo
• E. Errado

Uma torneira enche um tanque em 12 horas. Outra torneira enche o mesmo tanque em 15 horas. Sabendo-se que as duas torneiras foram abertas simultaneamente, que o tanque estava vazio quando as torneiras foram abertas, e que ao se atingir a metade da capacidade do tanque a segunda torneira foi fechada, o tempo total para encher o tanque é de

• A.

  seis horas e quarenta minutos.

• B.

  sete horas e meia.

• C.

  oito horas e vinte minutos.

• D.

  dez horas e dez minutos.

• E.

  nove horas e vinte minutos.

No teatro da escola de Fábio há 13 fileiras com 15 poltronas e mais 14 fileiras com 16 poltronas em cada uma. O total de poltronas do teatro é de:

• A. 408 poltronas.
• B. 419 poltronas.
• C. 405 poltronas.
• D. 412 poltronas.

Texto para as questões 53 e 54

A situação matemática descrita no texto caracteriza a situação denominada

• A.

  adidática de ação.

• B.

  adidática de formulação.

• C.

  adidática de validação.

• D.

  didática.

Considere o sistema linear S: 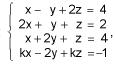    em que x, y e z são incógnitas reais.

Se S admite uma única solução, então a constante k é um número real

• A.

  negativo.

• B.

  quadrado perfeito.

• C.

  divisível por 3.

• D.

  primo.

• E.

  racional não inteiro.

Cinco números estão em progressão aritmética crescente, e o primeiro deles, o segundo e o quinto estão em progressão geométrica. Supondo que todos esses cinco números são maiores que 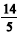 e menores que 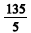e que a razão da progressão aritmética é um número inteiro, julgue os itens seguintes.

A soma desses cinco números é superior a 78.

• C. Certo
• E. Errado

Considerando a função y = f (x) = x² – 5x + 6, em um sistema de coordenadas cartesianas ortogonais xOy, julgue os itens que se seguem. A reta tangente ao gráfico de f no ponto de abcissa x = -1 forma com os eixos coordenados um triângulo de área superior a 2 unidades de área.

• C. Certo
• E. Errado

Considere uma função f:D→ R , definida no domínio D=(−∞,0)∪(0,3)∪(3,+∞). Em seu domínio, a função f é contínua e tem derivadas contínuas até a ordem 2. As retas x = 0 e x = 3 são assíntotas verticais de f e a reta y = 1 é assíntota horizontal de f. O gráfico da f é apresentado na figura abaixo.

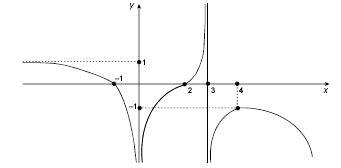
Com base no gráfico de f e nas informações acima, assinale a opção correta.

• A.

  

• B.

  A função f não muda de concavidade.

• C.

  Se x ∈ (0,3) então f (x)× f′(x)>0 .

• D.

  A função f é injetiva.

• E.

  Se x∈(3,+ ∞) então f ′(x)≠0 .