Questões de Matemática do ano 2007

Em certa cidade, os táxis cobram um preço fixo (bandeirada) de R$ 5,60 mais um determinado valor por quilômetro rodado. O gráfico mostra a relação entre o número de quilômetros rodados e o preço a ser pago. Para 10 quilômetros rodados, o preço será de

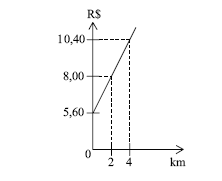
• A.

  R$ 40,00.

• B.

  R$ 30,80.

• C.

  R$ 22,70.

• D.

  R$ 17,60.

• E.

  R$ 15,20.

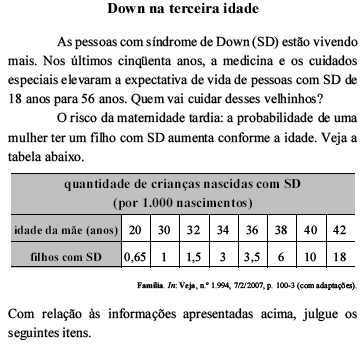
Em um sistema de coordenadas cartesianas xOy, os pontos de coordenadas (38, 6), (40, 10) e (42, 18), correspondentes aos três últimos elementos da tabela, estão sobre o gráfico de uma parábola de equação y = ax² + bx + c, em que a, b e c são constantes reais.

• C. Certo
• E. Errado

A equação algébrica x²+ bx – 1 = 0 tem duas raízes x¹ e x² tais que x²₁ + x² ₂ = 1. Pode-se afirmar que

• A.

  b = 1 ou b = –1

• B.

  b = 2 ou b = –2

• C.

  b = 0

• D.

  b = 2i ou b = –2i

• E.

  b = i ou b = – i

A figura representa parte do gráfico de uma função periódica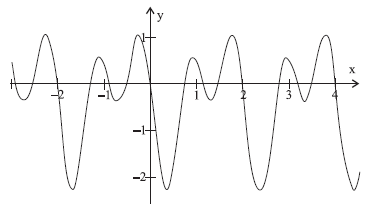

O período da função g(x) = f (3x+1) é

• A.

  1/3.

• B.

  2/3.

• C.

  2.

• D.

  3.

• E.

  6.

Parte do gráfico de uma função f está representado na figura.

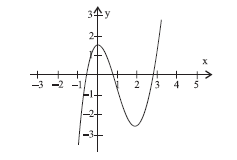
O gráfico que melhor representa g(x) = f(x – 1/2) + 1 é

• A.

• B.

• C.

• D.

• E.

Numa cidade com cerca de 5 milhões de habitantes, realiza- se uma pesquisa em laboratório em que uma cultura de bactérias é mantida com alimento ilimitado e sem inimigos. Sabendo-se que o número de bactérias presentes num certo instante t_o é igual a 100 e que esse número dobra de valor a cada hora transcorrida, o primeiro instante (em horas), após t_o, no qual a população de bactérias ultrapassará a população da cidade é

• A.

  menor ou igual a 10 horas.

• B.

  maior do que 10 horas, porém, menor ou igual a 20 horas.

• C.

  maior do que 20 horas, porém, menor ou igual a 24 horas.

• D.

  maior do que 24 horas, porém, menor ou igual a 48 horas.

• E.

  maior do que 48 horas.

Para cada inteiro positivo n, seja f(n) o resto da divisão de n por 5. Por exemplo, f(11) = 1, pois na divisão de 11 por 5, o resto é 1 e f(2) = 2, pois na divisão de 2 por 5, o quociente é 0 e o resto é 2. Então, pode-se afirmar que

• A.

  f(4n) = 3, para todo n.

• B.

  a imagem da função f é o conjunto dos números inteiros positivos.

• C.

  f(5n) = 5f(n), para todo n.

• D.

  f é uma função injetora.

• E.

  f (f(n)) = f(n), para todo n.

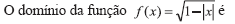
• A.

• B.

• C.

• D.

• E.

O coeficiente c da função 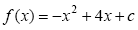 deve ser escolhido aleatoriamente entre os elementos do conjunto {-10, -9, -8,...,8, 9, 10} formado pelos números inteiros de −10 a 10. A probabilidade da função f apresentar duas raízes reais e distintas é:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja f a função que associa a cada número real x o menor elemento do conjunto {1-x, 2x+4}. O valor máximo de f(x) é:

• A.

  -1

• B.

  1

• C.

  2

• D.

  3

• E.

  4