Questões de Matemática do ano 2007

Texto para as questões 38 e 39

Considerando-se ainda as informações do texto e sabendo-se que a

população modelada por P(t), em 2006, era igual a 120.000 habitantes,

então o valor de k na expressão apresentada é igual a

• A.

  

• B.

  

• C.

  

• D.

  

Considere que, na fabricação de um lote de cadeiras do tipo

• A.

  300

• B.

  350

• C.

  400

• D.

  450

A função 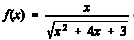 é válida para

• A.

  x > !1.

• B.

  x < 0.

• C.

  !2 < x < !1.

• D.

  !3 < x < !2.

Texto para as questões 38 e 39

Considerando as informações do texto, se e^k = 2 então a população estimada por P(t) para o ano de 2009 é igual a

• A.

  40.000.

• B.

  66.666.

• C.

  100.000.

• D.

  133.333.

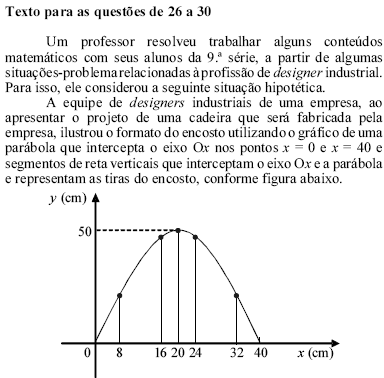
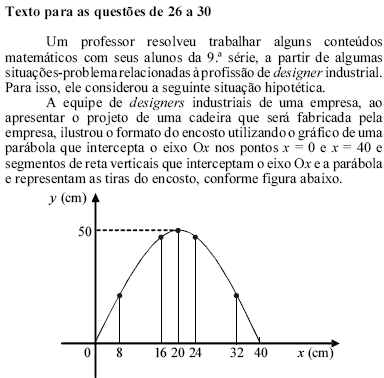
Com base no texto, é correto concluir que a soma dos comprimentos dos segmentos de reta que representam as tiras que serão utilizadas no encosto da cadeira projetada pela equipe de designers é, em metros, igual a

• A.

  1,20.

• B.

  2,10.

• C.

  4,50.

• D.

  5,70.

O conjunto que descreve o domínio máximo da função a valores reais dada por  é o subconjunto dos números reais satisfazendo a propriedade:

• A.

  −1≤ x ≤1 ou x ≥ 10

• B.

  −1≤ x ≤1 e x ≥ 10

• C.

  x ≤ − 1 ou x ≥10

• D.

  x ≤ − 1 e x ≥10

• E. x ≤ − 1 ou x ≥10 ou x ≥1

Considere a função tendo como domínio e contradomínio o conjunto dos números reais definida por f(x)=4^|x| e as seguintes afirmações sobre a mesma:

I- A função f é estritamente crescente ,

II- A função f possui inversa

III- O gráfico de f não corta o eixo x.

IV- O número real 2 pertence ao conjunto imagem de f.

São verdadeiras as afirmações:

• A.

  I e II

• B.

  II e III

• C.

  I e III

• D.

  III e IV

• E.

  II e IV

Observe uma possível seqüência de gráficos de y = ax² + bx + c.

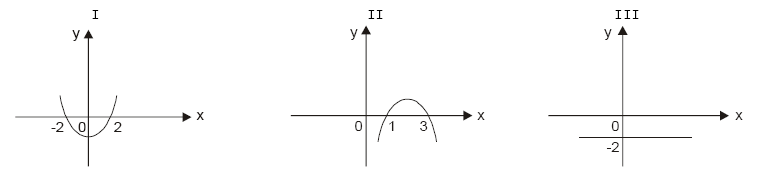
A seguir, observe três caracterizações para as constantes reais a, b e c:

i. a ≠ 0, b ≠ 0 e c ≠ 0
ii. a ≠ 0, b = 0 e c ≠ 0
iii. a = 0, b = 0 e c ≠ 0

A correta correspondência entre gráficos e valores das constantes reais a, b e c é

• A.

  I-i − II-iii − III-ii

• B.

  I-i − II-ii − III-iii

• C.

  I-ii − II-i − III-iii

• D.

  I-ii − II-iii − III-i

• E.

  I-iii − II-i − III-ii

Uma possibilidade para a introdução das idéias da álgebra é a identificação de padrões associada à representação com letras da regularidade observada. Nesse sentido, um professor propôs que seus alunos observassem o seguinte padrão:

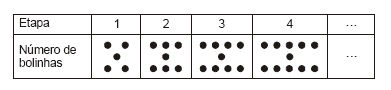
Chamando de E o número da etapa, e de B o número de bolinhas dessa etapa, partindo de caminhos diferentes, quatro alunos apresentaram as seguintes fórmulas para expressar a regularidade observada:

I. B = 2E + 3
II. B = 2 (E + 1) + 1
III. B = 3 (E + 1) − E
IV. B = 3 (E − 1) + 5

Das respostas apresentadas, estão corretas APENAS

• A.

  I e II.

• B.

  I e III.

• C.

  II e III.

• D.

  I, II e III.

• E.

  II, III e IV.

Um importante aspecto que deve ser trabalhado pelo professor no estudo de equações na última série do ensino fundamental refere-se ao seu conjunto universo. Admitindo-se a equação quadrática 2x² + x − 1 = 0, ela terá uma, e somente uma solução, se o seu conjunto universo for

• A.

  N.

• B.

  Z.

• C.

  Q.

• D.

  R-Q.

• E.

  R.