Questões de Matemática do ano 2008

Pesquisa feita entre alunos do ensino médio de escolas públicas revelou as atividades extra-curriculares de suas preferências: teatro, música, coral, dança e xadrez. Acerca dessa pesquisa, julgue os itens que se seguem.

Se o aluno puder escolher três dessas atividades, então ele terá 10 possibilidades de escolha.

• C. Certo
• E. Errado

Uma máquina realiza seis tipos de trabalho distintos, um após o outro, e as tarefas podem ser executadas em qualquer ordem. Nessa situação, o número de maneiras distintas que a máquina pode executar suas tarefas é igual a

• A.

  120

• B.

  210

• C.

  270

• D.

  720

Ferdinando desenhou uma bandeira composta de quatro listras horizontais e pediu a seu filho Zeca que a colorisse. Para tal, deu a Zeca três lápis de cor – nas cores preta, azul e vermelha – e as seguintes instruções: cada listra deve ser pintada com uma única cor; listras adjacentes (vizinhas) não podem ter a mesma cor. Nessas condições, de quantas maneiras distintas Zeca poderá colorir tal bandeira?

• A.

  36

• B.

  24

• C.

  20

• D.

  18

• E.

  10

Com relação a números e operações com números, julgue os seguintes itens.

A partir dos algarismos 1, 2, 4, 6, 8 e 9 é possível formar muitos pares de números de 3 algarismos, de modo que, para formar cada par, sejam usados todos esses algarismos. Somando os números de cada um desses pares, a maior soma que será possível obter é igual a 1.803.

• C. Certo
• E. Errado

Em uma urna há 5 bolas verdes, numeradas de 1 a 5, e 6 bolas brancas, numeradas de 1 a 6. Dessa urna retiram-se, sucessivamente e sem reposição, duas bolas. Quantas são as extrações nas quais a primeira bola sacada é verde e a segunda contém um número par?

• A.

  15

• B.

  20

• C.

  23

• D.

  25

• E.

  27

Há seis caminhos distintos que levam da cidade de Miacuda à cidade de Mipoupe; já para ir de Mipoupe a Deusmilivre, são sete os diferentes caminhos. Para ir de Miacuda a Deusmilivre, passando por Mipoupe há, portanto, a seguinte quantidade de diferentes itinerários:

• A.

  13;

• B.

  25;

• C.

  34;

• D.

  42;

• E.

  50.

Com relação a combinatória, cada um dos itens subseqüentes apresenta uma situação hipotética, seguida de uma assertiva a ser julgada.

Em um tribunal, deve ser formada uma comissão de 8 pessoas, que serão escolhidas entre 12 técnicos de informática e 16 técnicos administrativos. A comissão deve ser composta por 3 técnicos de informática e 5 técnicos administrativos. Nessa situação, a quantidade de maneiras distintas de se formar a comissão pode ser corretamente representada por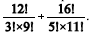

• C. Certo
• E. Errado

Com relação a combinatória, cada um dos itens subseqüentes apresenta uma situação hipotética, seguida de uma assertiva a ser julgada.

Em um tribunal, o desembargador tem a sua disposição 10 juízes para distribuir 3 processos para julgamento: um da área trabalhista, outro da área cível e o terceiro da área penal. Nesse tribunal, todos os juízes têm competência para julgar qualquer um dos 3 processos, mas cada processo será distribuído para um único juiz, que julgará apenas esse processo. Nessa situação, o desembargador tem mais de 700 formas diferentes para distribuir os processos.

• C. Certo
• E. Errado

Com relação a contagem, cada um dos próximos itens apresenta uma situação hipotética, seguida de uma assertiva a ser julgada.

Em um tribunal, os processos são protocolados com números de 6 algarismos de 0 a 9 e o primeiro algarismo refere-se ao número da sala onde o processo foi arquivado. Nessa situação, o total de processos que podem ser arquivados nas salas de números 4 e 5 é superior a 300.000.

• C. Certo
• E. Errado

Uma turma de 20 formandos é formada por 10 rapazes e 10 moças. A turma reúne-se para formar uma comissão de formatura composta por 5 formandos. O número de diferentes comissões que podem ser formadas, de modo que em cada comissão deve haver 3 rapazes e 2 moças, é igual a:

• A.

  2500

• B.

  5400

• C.

  5200

• D.

  5000

• E.

  5440