Questões de Matemática do ano 2009

Com relação ao sistema ,

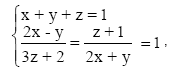
onde 3z +2≠0 e 2x+y≠0, pode-se, com certeza, afirmar que:

• A.

  é impossível.

• B.

  é impossível.

• C.

  possui determinante igual a 4.

• D.

  possui apenas a solução trivial.

• E.

  é homogêneo.

Considere uma esfera, um cone, um cubo e uma pirâmide. A esfera mais o cubo pesam o mesmo que o cone. A esfera pesa o mesmo que o cubo mais a pirâmide. Considerando ainda que dois cones pesariam o mesmo que três pirâmides, quantos cubos pesa a esfera?

• A.

  4

• B.

  5

• C.

  3

• D.

  2

• E.

  1

Dos 50 funcionários que participaram de um curso sobre a utilização de sistemas aplicativos das atividades meio e fim do Tribunal de Contas do Estado de São Paulo, sabese que:

– todos eram formados em Ciência da Computação ou em Engenharia de Software, mas apenas em um dos cursos;

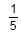–   do número de mulheres eram formadas em Engenharia de Software e  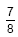do número de homens eram formados em Ciência de Computação.

Assim sendo, nesse curso, o total de participantes formados em Engenharia de Software era

• A.

  23

• B.

  17

• C.

  13

• D.

  9

• E.

  7

Sabendo-se que:

• A.

  1080

• B.

  1344

• C.

  756

• D.

  1020

Uma empresa de turismo fechou um pacote para um grupo de 80 pessoas, com o qual ficou acordado que cada pessoa que participasse pagaria R$ 1.000,00 e cada pessoa que desistisse pagaria apenas uma taxa de R$ 150,00. Se a empresa de turismo arrecadou um total de R$ 59.600,00, qual a porcentagem das pessoas que desistiram do pacote?

• A.

  20%

• B.

  24%

• C.

  30%

• D.

  42%

• E.

  36%

Pedro distribuiu um número x de moedas de 1 real em caixa numeradas de 1 à 5. Sabe-se que:

I. A quantidade de moedas na caixa 1 é o dobro da quantidade de moedas na caixa 2 e metade da quantidade de moedas na caixa 3

II. A diferença entre a quantidade de moedas nas caixas 5 e na caixa 4 é igual a quantidade de moedas na caixa 2

III. A caixa 5 tem 50 moedas e a caixa 3 tem 40 moedas.

Podemos dizer que a quantidade total de moedas (x) é igual a:

• A.

  150

• B.

  170

• C.

  140

• D.

  160

Classifique o sistema

• A.

  (1, 2, 3)  SPD

• B. (1, 2, 3) SI
• C.

  (2, 1, 3) SPD

• D.

  (2, 1, 3) SPI

O conjunto solução do sistema  é:

• A.

  S{(1, 1)}

• B.

  S{(2, 1)}

• C.

  S{(2, 2)}

• D.

  S{(1, 2)}

Zeus é um aficionado em matemática, pois quando lhe perguntaram sobre sua idade, ele respondeu: "Para saber a minha idade você deve decifrar o criptograma aritmético seguinte, que corresponde, de modo codificado, à adição de dois números naturais. Decifrado o criptograma, a minha idade é igual à soma dos algarismos que correspondem às letras da palavra FISCO."

Considerando que letras distintas correspondem a algarismos distintos, quantos anos tem Zeus?

• A.

  25

• B.

  24

• C.

  30

• D.

  22

• E.

  28

Godofredo e Lili aniversariam nos respectivos meses de agosto e setembro, em um mesmo dia da semana. Se o dia do aniversário de Godofredo é o sêxtuplo do dia do de Lili, então a soma das datas em que os dois aniversariam é

• A.

  28

• B.

  35

• C.

  7

• D.

  14

• E.

  21