Questões de Matemática do ano 2013

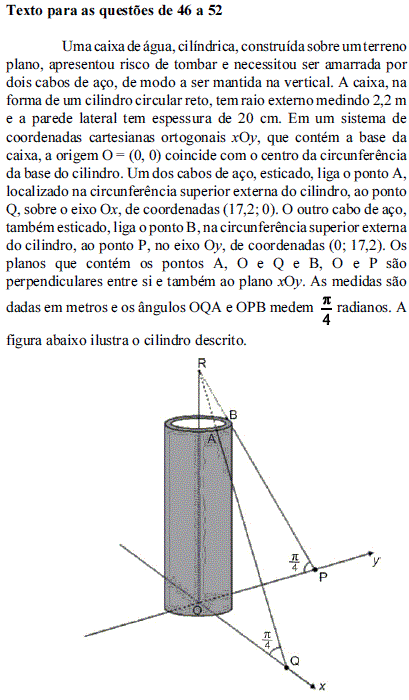
A equação cartesiana da reta que passa pelos pontos P e Q pode ser expressa por

• A.

  172x +10y = 0.

• B.

  5x + 5y = 86.

• C.

  5x – 5y = 86.

• D.

  -5x + 5y = 86.

• E.

  5x + 5y = -86.

Considere que, na pintura da parte lateral externa da caixa de água, seja empregada uma tinta especial à razão de 1 L de tinta para cada 2 m2. Nessa situação, considerando 3,14 como valor aproximado para π, se a tinta é vendida em latas de 5 L e se a sobra de tinta deve ser mínima, a quantidade de latas que deverão ser compradas para completar o serviço é igual a

• A.

  20.

• B.

  21.

• C.

  22.

• D.

  23.

• E.

  24.

Se o fundo da caixa coincidir com o nível do solo, então a capacidade da caixa de água será igual a

• A.

  15ð m³.

• B.

  20ð m³.

• C.

  60ð m³.

• D.

  68,8ð m³.

• E.

  72,6ð m³.

No sistema de coordenadas cartesianas considerado, para x > 0, os gráficos de f e de g limitam regiões com áreas finitas e que estão no primeiro quadrante. A respeito dessas áreas, representadas, respectivamente, por A(f) e A(g), assinale a opção correta.

• A.

  A(f) > A(g).

• B.

  A(f) = A(g).

• C.

  A(f) < 6.

• D.

  A(g) < 9.

• E.

  6 < A(f) < A(g) < 78.

A respeito dos valores máx f = valor máximo de f(x) e máx g = valor máximo de g(x), assinale a opção correta.

• A.

  máx f > máx g.

• B.

  0 < máx f < máx g < 2.

• C. 2 < máx f < máx g < 6.
• D.

  6 < máx f < máx g < 10.

• E.

  máx f = máx g.

Se a distância x for expressa por x = x(t) = v × t, em que t é o tempo, em segundos, 0 < t < 4, e v é uma constante positiva, então, no arremesso 1, a altura do peso em função do tempo será dada por y = y(t) = f(x(t)). Nessa situação, a altura máxima do peso ocorrerá no instante t₀ igual a

• A.

  4.

• B.

  4/v.

• C.

  v.

• D.

  v/4.

• E.

  4v.

Considere que os pesos usados nas aulas sejam esferas constituídas de um mesmo material: os alunos usam pesos de massa igual a 7,2 kg e com 12 cm de diâmetro; as alunas usam pesos de massa igual a 4 kg. Se, independentemente de usados por alunos ou por alunas, as massas dos pesos forem diretamente proporcionais aos volumes, então o raio do peso usado pelas alunas será igual a

• A.

  

• B.

  

• C.

  

• D.

  1,8 cm.

• E.

  

Se, para cada x, h(x) é a distância, em metros, que o peso está do solo, medida do ponto em que se encontra o peso até o ponto de coordenadas (x, 0), então, no arremesso 1, h(x) > 2,4 m para todo x, tal que

• A.

  0 < x < 2.

• B.

  0 < x < 4.

• C.

  x > 2.

• D.

  2 < x < 6.

• E.

  x > 6.

Se os valores de x correspondentes aos pontos em que o peso atingiu o solo em cada um dos 3 arremessos formam uma progressão geométrica crescente, então, no terceiro arremesso, temse que

• A.

  x = 9 m.

• B.

  x = 16,90 m.

• C.

  x =18 m.

• D.

  x = 25,35 m.

• E.

  x = 27 m.

Com base no texto acima, é correto afirmar que o peso atingiu a altura máxima quando

• A.

  x = 4 m no primeiro arremesso e x = 6 m no segundo arremesso.

• B.

  x = 8 m no primeiro arremesso e x = 12 m no segundo arremesso.

• C.

  x = 10 m no primeiro arremesso e x = 13 m no segundo arremesso.

• D.

  x = 12 m no primeiro arremesso e x = 18 m no segundo arremesso.

• E.

  x = 30 m no primeiro arremesso e x = 19,5 m no segundo arremesso.