Questões de Matemática do ano 2015

O relógio A marca exatamente 1 hora e 25 minutos. No mesmo instante o relógio B marca exatamente 1 hora e 23 minutos. O relógio A é um relógio que atrasa 10 segundos por hora. O relógio B adianta 10 segundos por hora. O tempo, medido corretamente, necessário para que o horário do relógio B esteja 1 minuto e 30 segundos à frente do horário do relógio A é de

• A. 10 horas e 30 minutos.
• B. 11 horas e 45 minutos.
• C. 9 horas e 20 minutos.
• D. 11 horas e 15 minutos.
• E. 10 horas e 20 minutos.

Para calcular o teor calórico de alimentos fritos, Carlos está analisando dois métodos de fritura: o método tradicional, com óleo de cozinha e o método de fritura sem óleo. A batata, por exemplo, possui, em média, 77 kcal por 100 gramas. Ao fritá‐la, utilizando o método tradicional, passa a ter 312 kcal por 100 gramas, com acréscimo calórico devido ao óleo de cozinha utilizado. Sabe‐se que, no processo de fritura, independente do método utilizado, a batata perde cerca de 70% de seu peso – sua parte que é constituída por água. Dessa forma, após a fritura utilizando‐se o método de fritura sem óleo, 100 gramas de batata passarão a ter, aproximadamente:

• A. 112 kcal.
• B. 184 kcal.
• C. 218 kcal.
• D. 256 kcal.

Fabrício possui um cofre com moedas de R$ 0,50 e R$ 1,00. Considerando que nesse cofre existem, no total, 250 moedas e que 4/10 são de R$ 1,00, então o número de moedas de R$ 0,50 que se precisa retirar para que o valor restante no cofre seja de R$ 128,00 é

• A. 94.
• B. 96.
• C. 99.
• D. 100.

Em um acampamento onde 33 alunos estão passando as férias de verão, 16 gostam de jogar futebol, 15 gostam de praticar trilha na mata e 12 gostam de ambas as atividades. Dessa forma, o número de alunos que não gostam de jogar futebol nem praticar trilha na mata é

• A. 13.
• B. 14.
• C. 15.
• D. 16.

Em uma viagem, um carro gasta 27 horas para ir de uma cidade A para a cidade B. Sabe‐se que a distância entre essas cidades é 2.160 km e que, mantendo‐se a mesma velocidade média e partindo da cidade B, esse carro chega à cidade C em 4,7 horas. Logo, a distância entre as cidades B e C é, em km:

• A. 284.
• B. 324.
• C. 376.
• D. 459.

Pedalando de segunda a sexta‐feira, um grupo de seis ciclistas percorre, no total, 500 km (somando‐se o trajeto percorrido por cada ciclista). Dessa forma, para alcançar o total de 900 km percorridos, o número de ciclistas necessários, pedalando de terça a domingo e mantendo‐se a mesma carga horária diária e velocidade média, será

• A. 8.
• B. 9.
• C. 10.
• D. 12.

Na conta bancária de Júlio foram feitas quatro movimentações: primeiramente três depósitos e, por fim, um saque. Sabe‐se que os depósitos formam, na ordem de sua ocorrência, uma progressão aritmética crescente e que, após o saque, sua conta ficou com R$ 200,00 a mais do que havia inicialmente. Considerando que o valor do saque foi R$ 700,00, então o valor do segundo depósito foi

• A. R$ 150,00.
• B. R$ 200,00.
• C. R$ 300,00.
• D. R$ 450,00.

A sequência numérica 1, 24, 116, 484, 1 956, … obedece, a partir do segundo elemento, a uma lei de formação do tipo a_{n + 1} = x.a_n + y, com x, y e n naturais e n maior ou igual a 1. O próximo elemento dessa sequência é

• A. 7 844.
• B. 7 895.
• C. 7 945.
• D. 7 994.
• E. 8 003.

Em um grupo composto por X pessoas, os que têm curso de ensino superior cursaram administração de empresas ou ciências econômicas, apenas. Das X pessoas, sabe-se que exatamente 150 cursaram administração de empresas, que exatamente 100 cursaram administração de empresas e ciências econômicas, que exatamente 230 cursaram apenas um desses dois cursos, e que exatamente 110 não cursaram ciências econômicas. Sendo assim, é possível afirmar, corretamente, que o valor de X é

• A. 360.
• B. 370.
• C. 380.
• D. 390.
• E. 400.

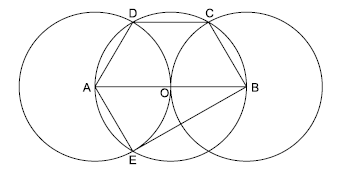
Na figura, estão representados um trapézio ABCD, um triângulo ABE e três circunferências com centros nos pontos A, O e B, de mesmo raio. Sabendo-se que as circunferências de centro A e B são tangentes no ponto O, que os pontos A, B, C, D e E pertencem à circunferência de centro O, e que os pontos C, D e E pertencem a duas das circunferências representadas, é possível afirmar corretamente que a razão entre os perímetros do trapézio ABCD e do triângulo ABE é:

• A.
• B.
• C.
• D.
• E.