Questões sobre Cilindros

A figura acima ilustra duas latas de leite condensado. A lata 1 é um cilindro circular reto de altura igual a 8 cm e diâmetro da base igual a 6 cm. A lata 2 é a sobreposição de 3 cilindros circulares retos: o inferior e o superior têm diâmetro da base igual a 6 cm e altura igual a 3 cm; o do meio tem altura igual a 2 cm e diâmetro da base igual a 4 cm.

Com base nessas informações, e na figura, julgue os itens a seguir.

Considere uma nova lata de leite condensado, de forma semelhante à da lata 2, em que se duplicou a altura do cilindro central e as demais medidas foram preservadas. Nessa situação, a lata 1 e essa nova lata têm a mesma capacidade.

• C. Certo
• E. Errado

A figura acima ilustra duas latas de leite condensado. A lata 1 é um cilindro circular reto de altura igual a 8 cm e diâmetro da base igual a 6 cm. A lata 2 é a sobreposição de 3 cilindros circulares retos: o inferior e o superior têm diâmetro da base igual a 6 cm e altura igual a 3 cm; o do meio tem altura igual a 2 cm e diâmetro da base igual a 4 cm.

Com base nessas informações, e na figura, julgue os itens a seguir.

• C. Certo
• E. Errado

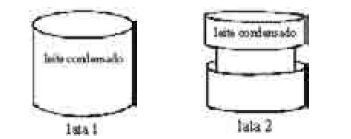
A figura acima ilustra duas latas de leite condensado. A lata 1 é um cilindro circular reto de altura igual a 8 cm e diâmetro da base igual a 6 cm. A lata 2 é a sobreposição de 3 cilindros circulares retos: o inferior e o superior têm diâmetro da base igual a 6 cm e altura igual a 3 cm; o do meio tem altura igual a 2 cm e diâmetro da base igual a 4 cm.

Com base nessas informações, e na figura, julgue os itens a seguir.

A razão entre o volume da lata 1 e o volume da lata 2 é igual a 36/31.

• C. Certo
• E. Errado

Deseja-se construir um reservatório na forma de um cilindro circular reto, sem tampa superior, com capacidade para 50.000 litros de petróleo. As paredes do reservatório serão feitas de aço com 1 cm de espessura. Esse material será usado tanto na base como nas paredes laterais do reservatório. O objetivo é construir um reservatório que tenha a capacidade exigida e que, na sua construção, necessite da menor quantidade possível de material.

 Julgue os itens que se seguem a respeito desse reservatório, considerando que x e h, em centímetros, sejam, respectivamente, o raio interno da base e a altura interna do cilindro, que correspondem às dimensões do espaço útil do reservatório.

Para ter a capacidade exigida, gastando-se a menor quantidade possível de aço na sua construção, o reservatório deve ser tal que h = 2x.

• C. Certo
• E. Errado

Para calcularmos o volume de um cilindro multiplicamos a área da base por sua altura. Num país fictício, a moeda mais valiosa tem a forma de um cilindro cuja base tem 1,5cm de diâmetro e cuja altura é 3mm.

O volume dessa moeda, em centímetros cúbicos, é aproximadamente igual a:

• A.

  0,034;

• B.

  0,53;

• C.

  1,4;

• D.

  5,2;

• E.

  12,6.

Uma lata de azeite (cilíndrica) tem 5cm de raio na base e 20cm de altura. O total de ml de azeite que cabem nessa lata é:

• A.

  1.570;

• B.

  1.750;

• C.

  1.507;

• D.

  1.758,5.

Um supermercado vende determinado suco de frutas acondicionado nos recipientes A e B, ambos tendo a forma de cilindro circular reto. A altura do recipiente A é o dobro da altura do recipiente B, e o diâmetro da base de A é a metade do diâmetro da base de B. No recipiente A, o preço do suco é igual a R$ 1,00 e, no recipiente B, R$ 1,50. Considerando apenas a quantidade de suco contida em cada recipiente, julgue os itens que se seguem.

Os dois recipientes contêm a mesma quantidade de suco.

• C. Certo
• E. Errado

Uma lata de forma cilíndrica contém 3 bolas esféricas de tênis que se tangenciam e tangenciam as tampas inferior e superior da lata. Suponha que o raio da base da lata é o mesmo que o raio das bolas de tênis. Então a razão entre o comprimento da circunferência da base e a altura do cilindro é:

• A.

  

• B.

  

• C.

  

• D.

  3

• E.

  

Com relação a um cilindro circular reto, cujo raio da base mede 2 m e de altura igual a 3 m, julgue os itens seguintes, considerando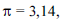 Considere que o cilindro era feito de madeira sólida e que tenha sido desbastado para se obter um cone circular sólido, de tal forma que a base coincidia com a base do cilindro e o vértice coincidia com o centro da face superior do cilindro. Nesse caso, é correto afirmar que, para se obter o cone, mais de 70% do volume do cilindro foi retirado.

• C. Certo
• E. Errado

Com relação a um cilindro circular reto, cujo raio da base mede 2 m e de altura igual a 3 m, julgue os itens seguintes, considerando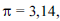 Desprezando-se a espessura das paredes, o volume do maior paralelepípedo retângulo de base quadrada e altura igual à altura do cilindro que pode ser inscrito nesse cilindro é superior a 25 m3.

• C. Certo
• E. Errado