Questões sobre Geometria Analítica

Considerando que o interior de um quarto tenha o formato de um paralelepípedo retângulo com altura de 3 metros e volume de 36 metros cúbicos, e que o piso desse quarto seja um retângulo cuja diagonal meça 5 metros, julgue os itens a seguir.

A distância máxima entre dois pontos das paredes do quarto é inferior a 6 metros.

• C. Certo
• E. Errado

Considerando a função y = f (x) = x² – 5x + 6, em um sistema de coordenadas cartesianas ortogonais xOy, julgue os itens que se seguem. A reta tangente ao gráfico de f no ponto de abcissa x = -1 forma com os eixos coordenados um triângulo de área superior a 2 unidades de área.

• C. Certo
• E. Errado

A equação que descreve altura y em função do raio x é uma reta paralela à reta que passa pelos pontos de coordenadas (1, 4) e (2, 2).

• C. Certo
• E. Errado

• C. Certo
• E. Errado

Em um sistema de coordenadas cartesianas ortogonais, considere o quadrado Q de vértices nos pontos (1, 0), (0, 1), (-1, 0) e (0, -1) e a região T compreendida entre os gráficos das funções f (x) = x² – 1 e g (x) = -x² + 1. Nesse caso, é correto afirmar que

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

No sistema de coordenadas cartesianas ortogonais, uma partícula executa um movimento circular uniforme cuja trajetória tem como diâmetro o segmento que une os pontos P = (1, 2) e Q = (2, -1). A equação cartesiana que descreve esse movimento é

• A.
• B.

  (2x - 3)² + (2y - 1)² = 10.

• C.
• D.
• E.

No sistema de coordenadas cartesianas ortogonais xOy, a equação 4x² + 16y² + 8x – 64y + 4 = 0 representa

• A.

  uma hipérbole de centro (-1, 2).

• B.

  uma elipse de centro (-1, 2).

• C.

  uma parábola de vértice (-1, 2).

• D.

  uma circunferência de centro (-1, 2).

• E.

  duas retas que se cruzam no ponto (-1, 2).

Considerando a função y = f (x) = x² – 5x + 6, em um sistema de coordenadas cartesianas ortogonais xOy, julgue os itens que se seguem.

Se P 1 = (x 1 , 0), P 2 = (x 2 , 0), em que x 1 < x 2 são as raízes da equação f (x) = 0 e se P 0 = (x 0 , y 0 ) é o ponto de mínimo do gráfico de f, então o volume do cone circular reto que tem o comprimento do segmento P 1 P 2 como diâmetro da base e cuja altura é *y 0* é superior a 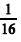 unidade de volume.

• C. Certo
• E. Errado

Considere que o deslocamento de um barco seja ser descrito em um sistema de coordenadas cartesianas xOy, em que x e y são dados em metros. No início do deslocamento, no instante t₀ = 0, o barco estava localizado no ponto P₁ = (200, 400), 8 minutos mais tarde, em t₁ = 8, a sua localização correspondia ao ponto P₂ (220, 340). Com base nessas informações, julgue os itens a seguir.

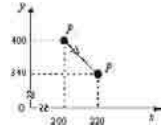
Pode-se representar corretamente o vetor velocidade média
do barco no intervalo de tempo referido acima por meio do
gráfico ilustrado a seguir.

• C. Certo
• E. Errado

Considere que o deslocamento de um barco seja ser descrito em um sistema de coordenadas cartesianas xOy, em que x e y são dados em metros. No início do deslocamento, no instante t₀ = 0, o barco estava localizado no ponto P₁ = (200, 400), 8 minutos mais tarde, em t₁ = 8, a sua localização correspondia ao ponto P₂ (220, 340). Com base nessas informações, julgue os itens a seguir.

As componentes da velocidade média do barco nas direções
1 0 Ox e Oy, no intervalo ) 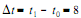 minutos, são maiores
que 0,4 m/s e 0,18 m/s, respectivamente.

• C. Certo
• E. Errado