Questões sobre Matrizes e Determinantes

Genericamente, qualquer elemento de uma matriz M pode ser representado por m_ij, onde i representa a linha e j a coluna em que esse elemento se localiza. Uma matriz X = x_ij, de terceira ordem é a matriz resultante da soma das matrizes A = (a_ij) e B = (b_ij). Sabendo-se que (a_ij ) = i²-j ² e que b_ij = (i+j)², então a soma dos elementos x₃₁ e x₁₃ é igual a:

• A.

  20

• B.

  24

• C.

  32

• D.

  64

• E.

  108

Na revista da Associação Brasileira das Empresas de Transporte Rodoviário Intermunicipal, Interestadual e Internacional de Passageiros (ABRATI), de março de 2002, foi publicada a tabela abaixo, que traz o número de mortes ocorridas na Rodovia Presidente Dutra, que liga a cidade do Rio de Janeiro à capital paulista, entre os anos de 1997 e 2000.

De acordo com um conhecido método da Matemática, denominado Método dos Quadrados Mínimos (MQM), esses valores podem ser ajustados (modelados) por uma função linear da forma f(t) = at + b. O ajuste da função, com os dados fornecidos na tabela, está esboçado no gráfico a seguir.

Para se conhecer os números reais a e b que definirão a função linear f(t) será necessário resolver o seguinte sistema de equações lineares, segundo o MQM:

Com base nessas informações, julgue os itens que se seguem.

O sistema (I) pode ser escrito na forma matricial como A × X = B, em que  , e B = Y × M é o produto das matrizes   .

• C. Certo
• E. Errado

Na revista da Associação Brasileira das Empresas de Transporte Rodoviário Intermunicipal, Interestadual e Internacional de Passageiros (ABRATI), de março de 2002, foi publicada a tabela abaixo, que traz o número de mortes ocorridas na Rodovia Presidente Dutra, que liga a cidade do Rio de Janeiro à capital paulista, entre os anos de 1997 e 2000.

De acordo com um conhecido método da Matemática, denominado Método dos Quadrados Mínimos (MQM), esses valores podem ser ajustados (modelados) por uma função linear da forma f(t) = at + b. O ajuste da função, com os dados fornecidos na tabela, está esboçado no gráfico a seguir.

Para se conhecer os números reais a e b que definirão a função linear f(t) será necessário resolver o seguinte sistema de equações lineares, segundo o MQM:

Com base nessas informações, julgue os itens que se seguem.

A matriz dos coeficientes do sistema (I) é obtida pelo produto  , das matrizes  .

• C. Certo
• E. Errado

O valor do determinante é:

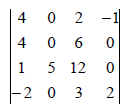
• A.

  – 40

• B.

  – 30

• C.

  – 20

• D.

  – 10

A representação explícita da matriz 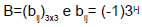 é dada por:

• A.
• B.
• C.
• D.

Uma matriz quadrada X de terceira ordem possui determinante igual a 3. Sabendo-se que a matriz Z é a transposta da matriz X, então a matriz Y = 3 Z tem determinante igual a

• A. 1/3
• B. 3
• C. 9
• D. 27
• E. 81

e sabendo que o determinante de sua matriz inversa é igual a 1/2, então o valor de X é igual a:

• A. -1
• B. 0
• C. 1/2
• D. 1
• E. 2

Seja A uma matriz n x n real e sua transposta A^t tal que A = A^t. Considere as afirmações abaixo:

I. Se n é par det(A) ≠ det(A^t)

II. Se n é ímpar det(A) = 0

III. det(A^t) = (- 1)ⁿ det(A)

Considerando V para afirmação verdadeira e F para afirmação falsa para a sequência I, II e III acima, marque a alternativa correta:

• A.

  V-F-V

• B.

  F-V-V

• C.

  F-F-V

• D.

  F-F-F

A matriz S = s_ij, de terceira ordem, é a matriz re-sultante da soma das matrizes A = (a_ij) e B=(b_ij). Sabendo-se que (a_ij ) = i²+j² e que b_ij = 2 i j, en-tão: a soma dos elementos s₃₁ e s₁₃ é igual a:

• A. 12
• B. 14
• C. 16
• D. 24
• E. 32

Genericamente, qualquer elemento de uma matriz M pode ser representado por m_ij, onde i representa a linha e j a coluna em que esse elemento se localiza. Uma matriz S = s_ij, de terceira ordem, é a matriz resultante da soma das matrizes A = (a_ij) e B = (b_ij). Sabendo-se que (a_ij ) = i²+j² e que b_ij = (i+j)², então a razão entre os elementos s₃₁ e s₁₃ é igual a:

• A. 1/5
• B. 2/5
• C. 3/5
• D. 4/5
• E. 1