Questões sobre Polinômios

Considere os polinômios p(x) = x ³ - 5x ² + 6x e d(x) = x - 3, e seja q(x) o quociente da divisão de p(x) por d(x), cujo resto é representado por r(x). Nesse caso, é correto afirmar que

p(x) não é divisível por d(x), isto é, para algum valor de x tem-se que r(x) … 0.

• C. Certo
• E. Errado

Para responder às questões 39, 40, 41 e 42, considere o teorema fundamental da álgebra: "Toda equação polinomial admite pelo menos uma raiz complexa".

O conhecimento desse teorema auxilia o professor do ensino fundamental, principalmente quando ministra aulas a respeito de

• A. geometria plana.
• B. razão e proporção.
• C. equações do 2º grau.
• D. operações com números inteiros.

Para responder às questões 39, 40, 41 e 42, considere o teorema fundamental da álgebra: "Toda equação polinomial admite pelo menos uma raiz complexa".

Considerando a função polinomial y = p x), podemos garantir que essa função possui um zero real, ou uma quantidade ímpar de zeros reais, se o polinômio p x) for de

• A. 4º grau.
• B. 2º grau.
• C. grau ímpar.
• D. grau superior a 3.

Para responder às questões 39, 40, 41 e 42, considere o teorema fundamental da álgebra: "Toda equação polinomial admite pelo menos uma raiz complexa". Esse teorema foi demonstrado primeiramente na tese de doutoramento de

• A. Isaac Newton.
• B. Niels Henrik Abel.
• C. Carl Friedrich Gauss.
• D. Évariste Galois.

Na figura abaixo, temos o esboço do gráfico da função y = p(x) ,

sendo p(x) um polinômio. Pode-se afirmar que p(x) é divisível por

• A. x − 2
• B. x + 3
• C. (x + 2)(x + 3)
• D. (x + 3)(x − 2)
• E. (x + 2)(x − 3)

Julgue o seguinte item, acerca de polinômios.

É possível encontrar números reais m e n tais que as raízes do polinômio q(x) = x² - 1 sejam também raízes do polinômio p(x) = x⁴ + (2m + n + 1)x³ + mx.

• C. Certo
• E. Errado

Com relação ao conjunto dos números reais, julgue o seguinte item.

No conjunto dos números reais, apenas  é solução da equação

• C. Certo
• E. Errado

Julgue os seguintes itens, acerca de polinômios.

Considerando-se a e b números reais, a equação polinomial x ³ + ax ² + bx + 1 = 0 sempre tem uma raiz real, independentemente dos valores de a e b.

• C. Certo
• E. Errado

Com relação ao conjunto dos números reais, julgue os seguintes itens.

No conjunto dos números reais, apenas X = 3/2 é solução da equação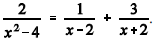 

• C. Certo
• E. Errado

Considerando, no sistema de coordenadas cartesianas xOy, os polinômios P(x) = x³ + x² + 5x - 1, Q(x) = x³ + 4x + 1 e R(x) = P(x) - Q(x), julgue os seguintes itens.

Se ", $ e ( são as raízes de Q(x), então "2 + $2 + (2 = !8, o que é suficiente para garantir que a equação Q(x) = 0 tenha uma única solução real.

• C. Certo
• E. Errado