Questões sobre Sistemas Lineares

Uma empresa de turismo fechou um pacote para um grupo de 80 pessoas, com o qual ficou acordado que cada pessoa que participasse pagaria R$ 1.000,00 e cada pessoa que desistisse pagaria apenas uma taxa de R$ 150,00. Se a empresa de turismo arrecadou um total de R$ 59.600,00, qual a porcentagem das pessoas que desistiram do pacote?

• A.

  20%

• B.

  24%

• C.

  30%

• D.

  42%

• E.

  36%

Pedro distribuiu um número x de moedas de 1 real em caixa numeradas de 1 à 5. Sabe-se que:

I. A quantidade de moedas na caixa 1 é o dobro da quantidade de moedas na caixa 2 e metade da quantidade de moedas na caixa 3

II. A diferença entre a quantidade de moedas nas caixas 5 e na caixa 4 é igual a quantidade de moedas na caixa 2

III. A caixa 5 tem 50 moedas e a caixa 3 tem 40 moedas.

 

Podemos dizer que a quantidade total de moedas (x) é igual a:

• A.

  150

• B.

  170

• C.

  140

• D.

  160

Classifique o sistema

• A.

  (1, 2, 3)  SPD

• B. (1, 2, 3) SI
• C.

  (2, 1, 3) SPD

• D.

  (2, 1, 3) SPI

O conjunto solução do sistema  é:

• A.

  S{(1, 1)}

• B.

  S{(2, 1)}

• C.

  S{(2, 2)}

• D.

  S{(1, 2)}

Quando Carlos e André se encontraram, Carlos tinha R$8,00 a mais que André. Como estava devendo certa quantia a André, Carlos aproveitou e pagou sua dívida. Assim, André passou a ter o dobro da quantia que tinha quando encontrou o amigo, e Carlos ficou com R$2,00 a menos do que tinha André antes de receber o pagamento. Qual a quantia, em reais, que Carlos pagou a André?

• A.

  6,00

• B.

  8,00

• C.

  10,00

• D.

  12,00

• E.

  14,00

Uma exposição de arte recebeu 510 visitantes, todos pagantes. Alguns pagaram R$ 6,00 pelo ingresso e outros, R$ 3,00, gerando uma arrecadação de R$ 2.490,00. Quantos foram os visitantes que pagaram ingressos de R$ 3,00?

• A.

  190

• B.

  210

• C.

  250

• D.

  280

• E.

  320

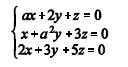
Considerando o sistema homogêneo de equações lineares apresentado acima, em que a é uma constante real, julgue os itens que se seguem.

Independentemente do valor de a, o sistema tem apenas a solução x = y = z = 0.

• C. Certo
• E. Errado

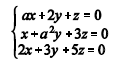
Considerando o sistema homogêneo de equações lineares apresentado acima, em que a é uma constante real, julgue os itens que se seguem.

Para a = -1, a única solução do sistema é x = y = z = 0.

• C. Certo
• E. Errado

A balança de dois pratos é um material concreto que auxilia na compreensão e resolução de equações. Considere, na figura abaixo, que objetos iguais representam pesos iguais e que todas as balanças estejam em equilíbrio.

Com relação a essas balanças, julgue os itens subseqüentes.

Designando por x, y e z, respectivamente, valores não-nulos do pentágono, do quadrado e da cruz, que mantêm o equilíbrio nas três balanças, então 4x + 2y + z = 0.

• C. Certo
• E. Errado

A balança de dois pratos é um material concreto que auxilia na compreensão e resolução de equações. Considere, na figura abaixo, que objetos iguais representam pesos iguais e que todas as balanças estejam em equilíbrio.

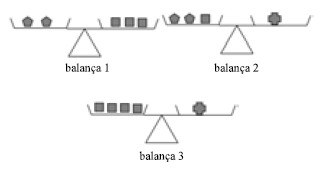
Com relação a essas balanças, julgue os itens subseqüentes.

Infere-se da figura que as equações representadas nas balanças 2 e 3 são equivalentes.

• C. Certo
• E. Errado