Questões sobre Sistemas Lineares

Uma lata de açaí custa R$ 3,00, se for de boa qualidade, e R$ 1,80, se for de qualidade inferior. Um agricultor colheu uma quantidade de latas do açaí de boa qualidade que excede em 15 latas à de qualidade inferior. Vendida essa colheita, o agricultor recebeu R$ 165,00. Com base nessas informações, julgue os itens subseqüentes.

O agricultor colheu menos de 20 latas do açaí de qualidade inferior.

• C. Certo
• E. Errado

Da folha de pagamento mensal de uma empresa, R$ 30.000,00 são destinados ao pagamento dos salários dos 8 empregados de nível A e dos 15 empregados de nível B. Sabendo que a diferença salarial de um empregado de nível A para um empregado de nível B é de R$ 300,00, julgue os itens seguintes.

O montante pago mensalmente aos empregados de nível salarial menor é superior a R$ 16.000,00.

• C. Certo
• E. Errado

Da folha de pagamento mensal de uma empresa, R$ 30.000,00 são destinados ao pagamento dos salários dos 8 empregados de nível A e dos 15 empregados de nível B. Sabendo que a diferença salarial de um empregado de nível A para um empregado de nível B é de R$ 300,00, julgue os itens seguintes.

A soma dos salários de um empregado de nível A e de um empregado de nível B é inferior a R$ 2.500,00.

• C. Certo
• E. Errado

Em um escritório com um total de 30 empregados, sabese que o salário médio dos homens é igual a R$ 2.000,00 e o das mulheres igual a R$ 1.500,00. O salário médio de todos os empregados é igual a R$ 1.800,00. Então, o número de homens, neste escritório, é igual a

• A.

  10

• B.

  12

• C.

  15

• D.

  16

• E.

  18

Em um tribunal, há 210 processos para serem analisados pelos juízes A, B e C. Sabe-se que as quantidades de processos que serão analisados por cada um desses juízes são, respectivamente, números diretamente proporcionais aos números a, b e c. Sabe-se também que a + c = 14, que cabem ao juiz B 70 desses processos e que o juiz C deverá analisar 80 processos a mais que o juiz A. Com relação a essa situação, julgue os itens seguintes.

c < 10.

• C. Certo
• E. Errado

Dois software, S1 e S2, são utilizados diariamente por participantes de diferentes grupos de trabalho em certa empresa. Um desses grupos de trabalho está interessado na fabricação de dois produtos, P1 e P2; a fabricação de cada unidade de P1 requer 2 horas de utilização de S1 e 3 horas de utilização de S2, enquanto a fabricação de cada unidade de P2 requer 3 horas de utilização de S1 e 4 horas de utilização de S2. Foi decidido que, por motivos estratégicos, o software S1 estará disponível a esse grupo de trabalho por 12 horas por dia, enquanto o software S2 estará disponível por 9 horas diárias a esse grupo de trabalho. Os pesquisadores desse grupo desejam saber quantas unidades de P1 e quantas unidades de P2 conseguem produzir nessas condições diariamente e observaram que uma maneira de saber isso seria resolver o sistema de equações lineares .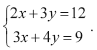

Com base nas informações acima, julgue os itens a seguir.

A solução do sistema de equações lineares fornece, de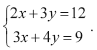 fato, uma possível quantidade a ser produzida de P1 e P2.

• C. Certo
• E. Errado

A razão entre as idades de dois técnicos é igual a 5/9. Se a soma dessas idades é igual a 70 anos, quantos anos o mais jovem tem a menos do que o mais velho?

• A.

  15

• B.

  18

• C.

  20

• D.

  22

• E.

  25

Um escritório possui um arquivo com muitas gavetas, utilizado para guardar processos, sendo que em cada gaveta o número de processos guardados equivale a seis vezes o número de gavetas desse arquivo. Se foi possível guardar, sem sobras, 864 processos nesse arquivo, então o número de processos em uma gaveta foi

• A.

  12.

• B.

  34.

• C.

  56.

• D.

  72.

• E.

  144.

Com certa quantidade de refrigerante é possível colocar 300 mL em cada copo não ocorrendo sobras. Se forem colocados 200 mL em cada copo, será possível encher 20 copos a mais com a mesma quantidade inicial de refrigerante, também não ocorrendo sobras. O número de copos enchidos com 200 mL foi

• A.

  80.

• B.

  60.

• C.

  40.

• D.

  20.

• E.

  10.

Acerca de sistemas de equações lineares com 3 equações e duas incógnitas, assinale a opção correta.

• A.

  Em um sistema de coordenadas cartesianas ortogonais, cada equação desse sistema representa uma reta.

• B.

  Sistemas lineares desse tipo não possuem solução.

• C.

  Esses sistemas podem ser resolvidos pela regra de Cramer.

• D.

  Esses sistemas podem ser resolvidos pela regra de Cramer.

• E.

  Algum sistema desse tipo, homogêneo, pode não ter solução.