Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Uma caixa retangular sem tampa será construída a partir da retirada de 4 quadrados de lado x cm de comprimento dos cantos de uma folha de papelão retangular de dimensões 30 cm × 20 cm, conforme mostra a figura I precedente. A figura II representa a caixa, após dobrarem-se as abas perpendicularmente à folha. O paralelepípedo reto (sem uma das faces) obtido tem altura de x cm.

A partir dessa situação, julgue os itens a seguir.

• C. Certo
• E. Errado

As figuras I e II a seguir ilustram recipientes cilíndricos retos, idênticos, que contêm suco. Em cada recipiente foram feitas marcações igualmente espaçadas, mas diferentes nos recipientes I e II. Há mais suco no recipiente I que no II.

Nessa situação, a fração do volume que o recipiente I tem a mais que o II é igual a

• A. 8/15.
• B. 8/13.
• C. 3/10.
• D. 4/3.
• E. 7/20.

O papiro Rhind é conhecido por apresentar problemas da matemática egípcia antiga. Datado de 1650 a.C., esse documento dispõe de uma coleção de soluções de 85 problemas de diversos campos da matemática, como aritmética e geometria. Também se encontra nessas escrituras a forma que os egípcios efetuavam multiplicações. Assinale a opção correspondente à multiplicação pelo método egípcio.

• A.

  Na multiplicação de 17 por 14, monta-se a tabela a seguir.

  

  Os elementos das células da primeira coluna são duplicados, um com relação ao anterior; os elementos da segunda coluna são a metade do número da célula anterior, caso o número seja par, e, caso seja ímpar, subtrai-se uma unidade e, então, divide-se por 2. As entradas na primeira coluna que ficam ao lado de entradas ímpares da segunda coluna são somadas produzindo-se, assim, o resultado da multiplicação: 34 + 68 + 136 = 238 = 17 × 14.

• B.

  Na multiplicação de 21 por 17, monta-se a tabela a seguir, em que ambos os fatores são escritos a partir de suas dezenas e unidades.

  

  As multiplicações entre todas as dezenas e unidades possíveis são realizadas, e o resultado final é a soma desses elementos, gerando-se a multiplicação desejada: 200 + 140 + 10 + 7 = 357 = 21 × 17.

• C.

  Para multiplicar 13 por 19, organizam-se as chamadas grades, cuja quantidade depende da quantidade de dígitos que compõem os números que se deseja multiplicar, como mostrado a seguir.

  

  Em cada quadradinho da grade, faz-se uma diagonal da direita para a esquerda formando-se as celas. Os dígitos do primeiro fator são escritos na primeira linha; e os do segundo fator, na coluna da direita, um em cada linha. Em cada cela, escreve-se o produto da multiplicação de um dígito pelo outro da seguinte forma: a diagonal de cada cela separa os dígitos que representam dezenas daqueles que representam unidades do produto obtido, por exemplo: 1 = 1 × 1 = 01; 3 = 3 × 1 = 03. Efetuadas todas as multiplicações, somam-se os números encontrados nas diagonais, da direita para a esquerda, que corresponde à soma: 7 + 30 + 20 + 90 + 100 = 247 = 13 × 19.

• D.

  Na multiplicação de 19 por 23, monta-se uma tabela como a seguir.

  

  Na primeira coluna, escrevem-se as potências de 2, começando-se por 1, até a potência correspondente ao número imediatamente anterior a um dos fatores, no caso, 16 = 24 < 19 < 32 = 25. Na segunda coluna, duplica-se sucessivamente o segundo fator. Na coluna das potências de 2, identificam-se as potências que fazem parte da representação binária do primeiro fator, no caso, 19 = 1 + 2 + 16. Em seguida, somam-se as respectivas duplicações na outra coluna, encontrando-se, assim, o produto desejado: 23 + 46 + 368 = 437 = 19 × 23.

• E. O método egípcio é realizado com as mãos. Em uma das mãos, abaixa-se a quantidade de dedos relativos a quanto o fator ultrapassa de 5. Na outra mão, repete-se o procedimento para o outro fator. Soma-se, assim, o número de dedos baixados, exprimindo-se a soma em dezenas. Seguidamente multiplicam-se os números de dedos levantados, o que fornece as unidades. Em seguida, somam-se as dezenas e unidades para que seja obtido o resultado.

Nesse sentido, o número sexagesimal “12,7;15,36” corresponde, na forma decimal, ao número

• A. 728,86.
• B. 1.288,60.
• C. 727,26.
• D. 128,86.
• E. 43.635,60.

Ainda com referência à situação apresentada no texto 11A3DDD, se for utilizado o desconto racional simples, o cliente deverá pagar, à vista,

• A. menos de R$ 920.
• B. mais de R$ 920 e menos de R$ 940.
• C. mais de R$ 940 e menos de R$ 960.
• D. mais de R$ 960 e menos de R$ 980.
• E. mais de R$ 980.

Na situação apresentada no texto 11A3DDD, se for utilizado o desconto comercial simples, o cliente deverá pagar, à vista, o valor de

• A. R$ 980.
• B. R$ 994.
• C. R$ 998.
• D. R$ 940.
• E. R$ 960.

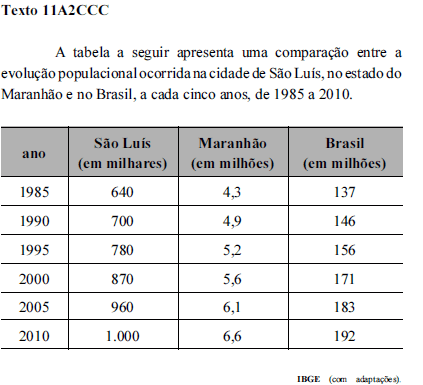Ainda com base na tabela do texto 11A2CCC, o desvio padrão da sequência dos três valores correspondentes à população brasileira nos anos de 2000, 2005 e 2010 é

• A. superior a 7 milhões e inferior a 9 milhões.
• B. superior a 9 milhões e inferior a 11 milhões.
• C. superior a 11 milhões e inferior a 13 milhões.
• D. superior a 13 milhões.
• E. inferior a 7 milhões.

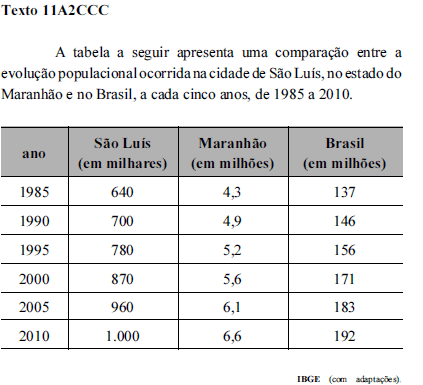Se a população do Maranhão crescer a cada quinquênio, a partir de 2010, de acordo com a progressão aritmética dos três valores correspondentes aos anos de 2000, 2005 e 2010 mostrados na tabela do texto 11A2CCC, então a população do Maranhão em 2090 será

• A. superior a 19,5 milhões.
• B. inferior a 15 milhões.
• C. superior a 15 milhões e inferior a 16,5 milhões.
• D. superior a 16,5 milhões e inferior a 18 milhões.
• E. superior a 18 milhões e inferior a 19,5 milhões.

Considerando essa situação hipotética, julgue os itens a seguir.

Sabendo-se que x = 30 é uma raiz da equação f(x) = 51.000, é correto afirmar que a primeira vez em que o programa A atingiu a marca de 51.000 telespectadores foi no vigésimo programa após a estreia.

• C. Certo
• E. Errado

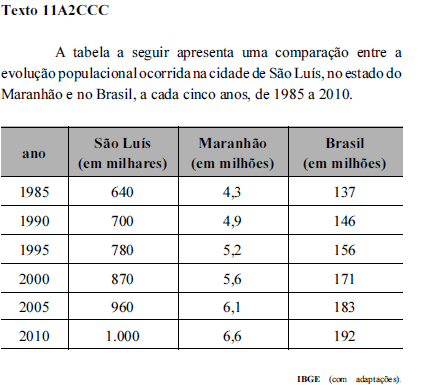Com base na tabela do texto 11A2CCC, considerando-se a sequência dos seis valores correspondentes à população de São Luís, infere-se que a mediana desses valores é igual a

• A. 725.000.
• B. 775.000.
• C. 825.000.
• D. 875.000.
• E. 700.000.