Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Um número ou palavra é denominado palíndromo se tem o mesmo significado quando se lê da esquerda para a direita ou da direita para a esquerda. Exemplos: a palavra arara e o número 1221 são palíndromos. A partir dessa definição, julgue os itens que se seguem.

Os números 12821 e 42724 são palíndromos e têm a mesma quantidade de unidades de milhar.

• C. Certo
• E. Errado

Um número ou palavra é denominado palíndromo se tem o mesmo significado quando se lê da esquerda para a direita ou da direita para a esquerda. Exemplos: a palavra arara e o número 1221 são palíndromos. A partir dessa definição, julgue os itens que se seguem.

Considere que um número tenha 6 algarismos, seja um palíndromo e possua 45 unidades de milhar. Então, nesse número, o algarismo 5 ocupa a casa das dezenas.

• C. Certo
• E. Errado

Um número ou palavra é denominado palíndromo se tem o mesmo significado quando se lê da esquerda para a direita ou da direita para a esquerda. Exemplos: a palavra arara e o número 1221 são palíndromos. A partir dessa definição, julgue os itens que se seguem.

O número formado por 32 dezenas e 15 unidades, quando somado ao número formado por 51 dezenas e 23 unidades, resulta em um palíndromo.

• C. Certo
• E. Errado

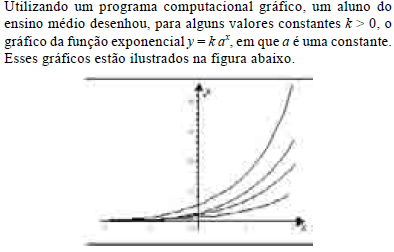
Com base nessas informações e na figura acima, julgue os itens a seguir.

• C. Certo
• E. Errado

Pierre Fermat, estudando os números primos, verificou que muitos deles poderiam ser escritos como a soma de dois quadrados perfeitos. Nesse sentido, uma professora pediu a seus alunos que construíssem exemplos de números primos que pudessem ser escritos como a soma de dois quadrados perfeitos. Ela explicou que os quadrados perfeitos são aqueles números que podem ser escritos como um produto da forma n × n, em que n é um número natural, e que números primos são aqueles que são divisíveis apenas pela unidade e por ele mesmo. As respostas abaixo foram dadas por alguns alunos.

Carla: 53 é primo e 53 = 49 + 4

Luíza: 47 é primo e 47 = 25 + 22

Pedro: 85 é primo e 85 = 49 + 36

 A partir dessas informações, julgue os itens a seguir.

A resposta de Pedro está de acordo com o que foi pedido pela professora.

• C. Certo
• E. Errado

Dos 27 empregados de uma empresa, x são mulheres e y são homens. Sabe-se que os números x e y são diretamente proporcionais a 4 e 5. Nesse caso, y - x é igual a

• A.

  6.

• B.

  5.

• C.

  4.

• D.

  3.

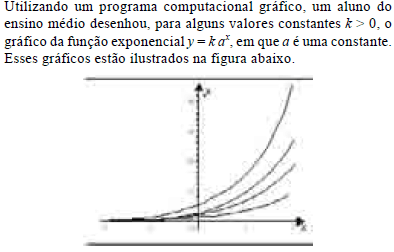
Com base nessas informações e na figura acima, julgue os itens a seguir.

Para uma mesma abscissa x, considere os pontos de coordenadas (x, k a^x ) para os diferentes valores de k. Nessa situação, o ponto que está mais próximo do eixo Ox é aquele que está sobre o gráfico da função em que o coeficiente k é o maior possível.

• C. Certo
• E. Errado

Pierre Fermat, estudando os números primos, verificou que muitos deles poderiam ser escritos como a soma de dois quadrados perfeitos. Nesse sentido, uma professora pediu a seus alunos que construíssem exemplos de números primos que pudessem ser escritos como a soma de dois quadrados perfeitos. Ela explicou que os quadrados perfeitos são aqueles números que podem ser escritos como um produto da forma n × n, em que n é um número natural, e que números primos são aqueles que são divisíveis apenas pela unidade e por ele mesmo. As respostas abaixo foram dadas por alguns alunos.

Carla: 53 é primo e 53 = 49 + 4

Luíza: 47 é primo e 47 = 25 + 22

Pedro: 85 é primo e 85 = 49 + 36

 A partir dessas informações, julgue os itens a seguir.

O exemplo de Luíza está de acordo com o que foi pedido pela professora.

• C. Certo
• E. Errado

Julgue os seguintes itens, relativos a sistemas lineares e equações de 1.º e de 2.º graus.

Se a soma de três números naturais consecutivos é igual a 72, então a soma de seus quadrados é inferior a 1.700.

• C. Certo
• E. Errado

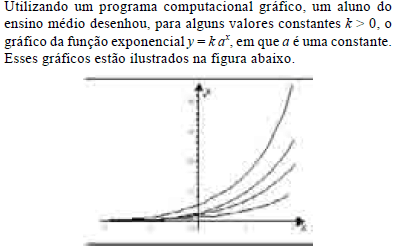
Com base nessas informações e na figura acima, julgue os itens a seguir.

Para cada valor de k o gráfico correspondente à função y = k a^x intercepta o eixo Oy no ponto de coordenadas (0, k).

• C. Certo
• E. Errado