Questões de Matemática da Núcleo de Computação Eletrônica UFRJ (NCE)

Um triângulo tem lados que medem 4,5cm, 6,0cm e 7,5cm. Em relação a esse triângulo é correto afirmar que:

• A.

  é retângulo;

• B.

  é isósceles;

• C.

  possui um ângulo obtuso;

• D.

  possui três ângulos agudos;

• E.

  é eqüilátero.

O produto das raízes da equação x² + 4x – 5 = 0, é igual a:

• A.

  – 4;

• B.

  4;

• C.

  5;

• D.

  5/4;

• E.

  – 5.

Na figura a seguir, os quatro triângulos sombreados são iguais, isósceles com ângulos 70^o, 70^o e 40^o.

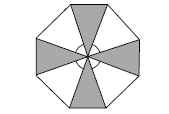
A soma dos ângulos indicados é igual a:

• A.

  120º;

• B.

  140º;

• C.

  150º;

• D.

  160º;

• E.

  200º.

Observe os triângulos ABC, ABD e ABE a seguir, em que C, D e E estão sobre uma mesma reta paralela à reta onde estão A e B:

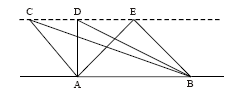
Se S1, S2 e S3 são as áreas dos triângulos ABC, ABD e ABE, respectivamente, então:

• A.

  S1 = S2 = S3;

• B.

  S1 > S2 > S3;

• C.

  S1 > S2 = S3;

• D.

  S1 < S2 < S3;

• E.

  S1 < S2 = S3.

Se 2x + 3y = 12 3x + 5y = – 6 então o produto xy é igual a:

• A.

  – 3.744;

• B.

  – 1.202;

• C.

  1;

• D.

  248;

• E.

  680.

• A.

  – 3.744;

• B.

  – 1.202;

• C.

  1;

• D.

  248;

• E.

  680.

Se 2x + 3y = 12 3x + 5y = – 6 então o produto xy é igual a:

• A.

  – 3.744;

• B.

  – 1.202;

• C.

  1;

• D.

  248;

• E.

  680.

Há seis caminhos distintos que levam da cidade de Miacuda à cidade de Mipoupe; já para ir de Mipoupe a Deusmilivre, são sete os diferentes caminhos. Para ir de Miacuda a Deusmilivre, passando por Mipoupe há, portanto, a seguinte quantidade de diferentes itinerários:

• A.

  13;

• B.

  25;

• C.

  34;

• D.

  42;

• E.

  50.

• A.

  2/45;

• B.

  6;

• C.

  30;

• D.

  48;

• E.

  90.

Um pentágono regular tem cinco diagonais, como mostra a figura a seguir:

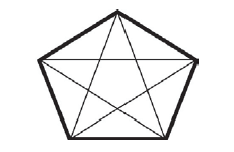
Um polígono regular com oito lados tem o seguinte número de diagonais:

• A.

  8;

• B.

  10;

• C.

  12;

• D.

  15;

• E.

  20.