Questões de Matemática da Núcleo de Computação Eletrônica UFRJ (NCE)

A pista de corrida onde Antenor treina para provas de longa distância circunda um parque com formato circular com 100m de raio. Já a pista onde Benedito treina circunda um parque com formato quadrado de 150m de lado. Comparando os comprimentos das duas pistas e as áreas ocupadas pelos dois parques concluímos que:

• A.

  tanto o comprimento da pista quanto a área do parque onde Antenor treina são maiores do que os correspondentes do parque onde treina Benedito;

• B.

  tanto o comprimento da pista quanto a área do parque onde Antenor treina são menores do que os correspondentes do parque onde treina Benedito;

• C.

  o comprimento da pista onde Antenor treina é maior do que o da pista onde treina Benedito, mas a área do parque é menor do que a de onde Benedito se exercita;

• D.

  o comprimento da pista onde Antenor treina é menor do que o da pista onde treina Benedito, mas a área do parque é maior do que a de onde Benedito se exercita;

• E.

  o comprimento da pista onde Antenor treina é maior do que o da pista onde Benedito treina, mas as áreas dos dois parques são iguais.

Na figura a seguir, B é o ponto médio do segmento AC.

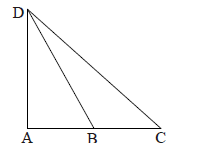
A razão entre as áreas do triângulo ABD e BCD é igual a:

• A.

  1;

• B.

  

• C.

  

• D.

  

• E.

  2

Um artista pintou um painel composto por quatro azulejos quadrados brancos, cada um deles com um quadrado inscrito pintado de cinza, como mostra a figura:

A razão entre a área branca e a área cinza é igual a:

• A.

  1;

• B.
• C.
• D.
• E.

Avalie as afirmativas a seguir, acerca de números:

I - Todo número natural é um número racional.

II - Todo número irracional é um número real.

III - Todo número real é um número racional.

IV - Todo número natural é um número inteiro.

Estão corretas somente as afirmativas:

• A.

  I e IV;

• B.

  II e III;

• C.

  I, II e III;

• D.

  I, II e IV;

• E.

  II, III e IV.

Um bilhão equivale a:

• A.

  dez vezes um milhão;

• B.

  cem vezes um milhão;

• C.

  mil vezes um milhão;

• D.

  cem mil vezes um milhão;

• E.

  um milhão vezes um milhão.

Se racionalizarmos o denominador de 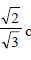 obtemos:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O professor pediu que cada aluno de uma turma pensasse em um número natural N, elevasse-o ao quadrado, somasse 5 ao resultado e anotasse, então, esse último número, que vamos chamar de X. Em seguida, cada aluno disse a um colega qual resultado X obtivera. O desafio do professor seria esse colega determinar o número natural N originalmente pensado pelo outro aluno. Para calcular o valor de N pensado pelo colega, a partir do valor X, o aluno deve fazer a seguinte conta:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O resultado de 5 + 30 ÷ 5 – 3 é:

• A.

  4;

• B.

  8;

• C.

  12;

• D.

  17;

• E.

  20.

Se f (x) = 2x – 10, então f (5) é igual a:

• A.

  0;

• B.

  2;

• C.

  4;

• D.

  6;

• E.

  10.

A derivada de f (x) =  no ponto x = 8 é igual a:

• A.

  1/3;

• B.

  4/3

• C.

  2/5

• D.

  5/3

• E.

  3/5