Questões de Raciocínio lógico da Fundação CESGRANRIO (CESGRANRIO)

Seis borrachas todas iguais e quatro lápis idênticos foram distribuídos por três gavetas de tal forma que, em cada uma das gavetas, há pelo menos uma borracha e um lápis. Sabe-se que, na gaveta que contém a maior quantidade de lápis, há mais borrachas do que em qualquer outra gaveta. Considerando-se que não há nenhum outro objeto nessas gavetas que não seja lápis ou borracha, pode-se afirmar, com certeza, que há alguma gaveta com exatamente

• A.

  seis objetos

• B.

  cinco objetos

• C.

  quatro objetos

• D.

  três objetos

• E.

  dois objetos

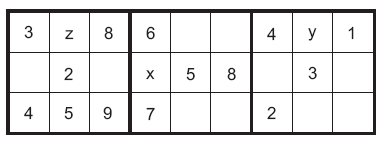
Um jogo é constituído de 27 quadrados numa grade de 3 x 9 quadrados. Essa grade é subdividida em 3 grades menores de 3 x 3 quadrados. Esses quadrados devem ser preenchidos com os números de 1 a 9, obedecidas as seguintes exigências:

- em cada uma das três fileiras horizontais, cada um dos números de 1 a 9 deve aparecer uma única vez;

- em cada uma das três grades menores, cada um dos números de 1 a 9 deve aparecer uma única vez.

Nestas condições, x + y + z vale

• A.

  16

• B.

  15

• C.

  13

• D.

  11

• E.

  10

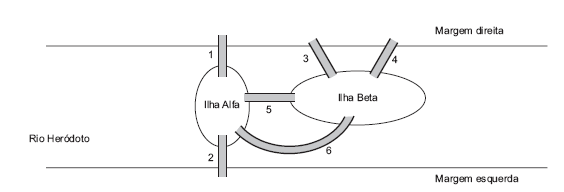
No rio Heródoto, há duas ilhas: Alfa e Beta. A ilha Alfa é ligada à margem direita pela ponte 1 e à margem esquerda pela ponte 2. A ilha Beta é ligada à margem direita pelas pontes 3 e 4, mas não é ligada à margem esquerda. Há ainda as ponte 5 e 6, que ligam uma ilha à outra. Percursos diferentes passando pelas pontes são caracterizados por seqüências diferentes formadas com números do conjunto {1, 2, 3, 4, 5, 6}. Por exemplo, (1,2) é um percurso que começa na margem direta, passa pela ponte 1, atravessa a ilha Alfa e, passando pela ponte 2, termina na margem esquerda. Note ainda que (1,5,3), (1,5,4) e (3,5,1) são diferentes percursos que saem da margem direita e chegam a essa mesma margem, passando pelas duas ilhas. O nº de percursos diferentes que podem ser feitos, começando na margem esquerda e terminando na margem direita, visitando necessariamente as duas ilhas sem que se passe por uma mesma ponte duas vezes, é

• A.

  menor do que 11.

• B.

  maior do que 11 e menor do que 15.

• C.

  maior do que 15 e menor do que 20.

• D.

  maior do que 20 e menor do que 25.

• E.

  maior do que 25.

A figura ilustra um tabuleiro do jogo RESTA UM. Começa-se o jogo com peças em todas as casas, exceto em uma, que está inicialmente vazia (Figura 1). Nesse jogo, todas as peças podem ser movimentadas. No entanto, cada casa comporta, no máximo, uma peça.

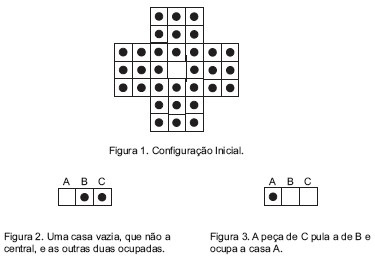
Nesse jogo, a única jogada possível consiste em: dadas três casas consecutivas em linha, na horizontal ou na vertical, se uma das casas, que não a central, estiver vazia e as outras duas, ocupadas, uma das peças salta a outra, adjacente, retirando-se do jogo a que foi pulada. Se não for possível realizar a jogada, o jogo acaba.

Na Figura 2, vê-se a casa A vazia e as casas B e C ocupadas. A peça que está em C pula a que está em B e passa a ocupar a casa A. A peça da casa B, que foi pulada, é retirada do jogo (Figura 3).

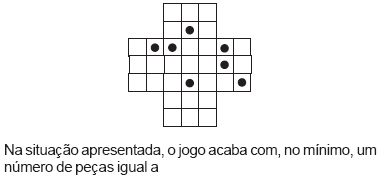
Abaixo, está representada uma situação de jogo no Resta Um.

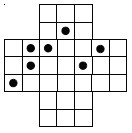
Na situação apresentada, o jogo acaba com, no mínimo, um número de peças igual a

Na situação apresentada, o jogo acaba com, no mínimo, um número de peças igual a

• A.

  1

• B.

  2

• C.

  3

• D.

  4

• E.

  5

Pedro está jogando com seu irmão e vai lançar dois dados perfeitos. Qual a probabilidade de que Pedro obtenha pelo menos 9 pontos ao lançar esses dois dados?

• A.
• B.
• C.
• D.
• E.

A turma de Marcelo foi dividida em 4 grupos. Cada grupo deverá fazer um trabalho sobre um derivado do petróleo: diesel, gasolina, nafta ou óleo combustível. Se a professora vai sortear um tema diferente para cada grupo, qual é a probabilidade de que o primeiro grupo a realizar o sorteio faça um trabalho sobre gasolina e o segundo, sobre diesel?

• A.
• B.
• C.
• D.
• E.

As 16 seleções de futebol que participarão das Olimpíadas de Pequim são divididas, para a primeira fase dos jogos, em quatro grupos com quatro times cada. Em cada grupo há um cabeça de chave, ou seja, um time previamente escolhido. Os outros três times são escolhidos por sorteio. A seleção brasileira é cabeça de chave de um dos grupos. Supondo que o sorteio dos times do grupo do Brasil fosse o primeiro a ser realizado, qual seria a probabilidade de que a seleção da China, país anfitrião dos jogos, ficasse no grupo do Brasil?

• A.
• B.
• C.
• D.

  

• E.

Antônio, Bianca, Carlos, Denise e Élton são colegas. Na tabela, o número 1 indica que a pessoa da linha tem o telefone da pessoa que está na coluna. Por sua vez, o número 0 indica que a pessoa da linha NÃO tem o telefone da pessoa que está na coluna. Assim, Denise tem o telefone de Carlos, mas Carlos não tem o telefone de Denise. Considerando-se que nenhum deles se opõe a fornecer o telefone de terceiros, o número mínimo de ligações telefônicas para que

• A. Antônio consiga falar com Denise é 3.
• B. Antônio consiga falar com Denise é 2.
• C. Bianca consiga falar com Carlos é 3.
• D. Carlos consiga falar com Denise é 2.
• E. Carlos consiga falar com Denise é 4.

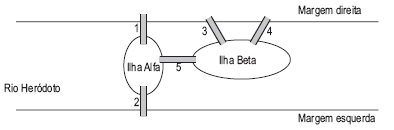
No rio Heródoto, há duas ilhas: Alfa e Beta. A ilha Alfa é ligada à margem direita pela ponte 1 e à margem esquerda pela ponte 2. A ilha Beta é ligada à margem direita pelas pontes 3 e 4, mas não é ligada à margem esquerda. Há ainda a ponte 5, que liga uma ilha à outra. Percursos diferentes passando pelas pontes são caracterizados por seqüências diferentes formadas com os números do conjunto {1,2,3,4,5}. Por exemplo, (1,2) é um percurso que começa na margem direita, passa pela ponte 1, atravessa a ilha Alfa e, passando pela ponte 2, termina na margem esquerda. Note ainda que (1,5,3), (1,5,4) e (3,5,1) são diferentes percursos que saem da margem direita e chegam a essa mesma margem, passando pelas duas ilhas. Quantos percursos diferentes podem ser feitos, que começam em uma margem e terminam na outra, visitando necessariamente as duas ilhas sem que se passe por uma mesma ponte duas vezes?

• A. 0
• B. 1
• C. 2
• D. 3
• E. 4

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5