Questões de Estatística

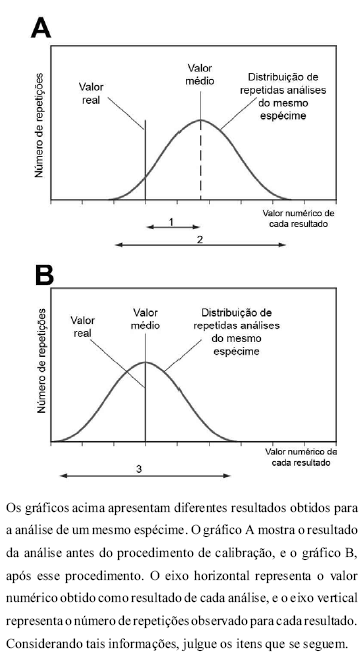
De acordo com os gráficos apresentados, a calibração foi um procedimento que não envolveu nenhuma modificação ou ajuste no sistema de análise.

• C. Certo
• E. Errado

Janaína ganhou de seus pais uma caixa com 12 canetas coloridas, todas com cores diferentes. Ela destampou as canetas, fechou os olhos, embaralhou as tampas e tampou-as novamente de forma aleatória. A esperança e a variância, respectivamente, do número de canetas que foram tampadas com sua tampa original são:

• A.

  1 e 5/12.

• B.

  1 e 11/12.

• C.

  1 e 1.

• D.

  6 e 3.

• E.

  6 e 30.

Dados do Instituto Brasileiro de Geografia e Estatística (IBGE) mostram que a participação percentual da região Norte na criação de gado registrou um crescimento muito acima do que nas outras regiões, o que preocupa os ambientalistas. Em 1990, menos de 10% do rebanho bovino nacional era da região Norte. Em 2006, esse percentual praticamente duplicou. Na região Centro-Oeste, onde pasta o maior número de cabeças de gado no Brasil, a participação no rebanho nacional passou de pouco mais de 30% para quase 35%. A figura a seguir apresenta a evolução temporal da participação de cada região no rebanho bovino brasileiro de 1990 a 2006. Os números são coletados pelo IBGE pela Pesquisa Pecuária Municipal.

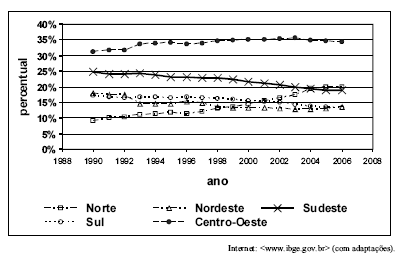
Com base nas informações do texto acima e considerando que as variáveis X_t, Y_t, W_t, Z_t e V_t, representam, respectivamente, os percentuais do rebanho nacional que existem nas regiões Norte, Nordeste, Sudeste, Sul e Centro-Oeste, no ano t, julgue os itens subseqüentes.

Previsões para 2007 e 2008 podem ser obtidas via filtro de Kalman, formulando-se um modelo na forma de espaço de estados.

• C. Certo
• E. Errado

A probabilidade de qualquer um deles ser contratado é 1/2

• C. Certo
• E. Errado

Tem-se que f(x)= C_n,x p^x(1-p)^n-x, onde C_n,x é o número de combinações de n elementos tomados x a x, é a função de probabilidade de uma variável aleatória binomial. Fazendo-se na sua expressão  , mas com  tem como limite a função de probabilidade de uma variável aleatória de Poisson, que é:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

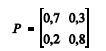
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

A cadeia é irredutível e aperiódica.

• C. Certo
• E. Errado

Um estudo para a estimação do número total, N, de usuários de drogas injetáveis foi realizado em um município no ano de 2006. A coleta de dados foi efetuada em duas fases por entrevistas face a face. A primeira fase (captura), que foi realizada nos meses de abril e maio de 2006, contou com n usuários entrevistados. A segunda fase (recaptura) foi realizada nos meses de agosto e setembro de 2006, com m usuários entrevistados. Com base nessas informações, considerando-se que N seja constante no período em questão e que todos os elementos da população tenham as mesmas chances de serem observados, julgue os itens subseqüentes.

Se r representa o número de recapturados, um estimador para N é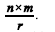

• C. Certo
• E. Errado

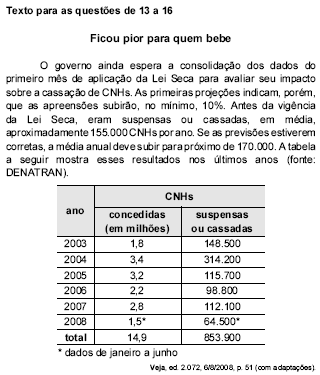
Para que a média de CNHs suspensas ou cassadas, de 2003 a 2008, atinja o valor previsto de 170.000, será necessário que, em 2008, a quantidade de CNHs suspensas ou cassadas seja um número

• A.

  inferior a 180.000.

• B.

  superior a 180.000 e inferior a 200.000.

• C.

  superior a 200.000 e inferior a 220.000.

• D.

  superior a 220.000 e inferior a 240.000.

• E.

  superior a 240.000.

Seja X uma variável aleatória com distribuição uniforme no intervalo (0,1) e suponha que a distribuição condicional de Y dado X = x seja binomial (n, x). Nesse caso, a esperança e a variância da variável aleatória Y são respectivamente:

• A.

  nx e nx(1 - x);

• B.

  

• C.

  

• D.

  

• E.

  

O vetor (X_min, X_max) é uma estatística suficiente minimal para δ.

• C. Certo
• E. Errado