Questões de Estatística

Os comprimentos de certos equipamentos são normalmente distribuídos com média 33,4cm e variância 1,44cm². A porcentagem de equipamentos que têm comprimentos inferiores a 31,2cm é aproximadamente igual a:

• A.

  1,0%;

• B.

  2,6%;

• C.

  3,4%;

• D.

  4,1%;

• E.

  5,0%.

Suponha que veículos passem por uma certa praça de pedágio de acordo com um processo Poisson a uma taxa média de 0,5 por minuto. A probabilidade de que passem mais de dois veículos num intervalo de dois minutos é aproximadamente igual a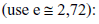

• A.

  0,08;

• B.

  0,16;

• C.

  0,32;

• D.

  0,64;

• E.

  0,92.

As lojas A e B fizeram uma promoção para a venda de CDs, e os preços pelas quantidades vendidas estão representados nos gráficos acima. Os gráficos das funções A(x) e B(x) representam, respectivamente, os preços em função das quantidades - x - de CDs compradas pelos clientes, nas lojas A e B. Cada um desses gráficos é formado por um segmento de reta e por uma semi-reta. A semi-reta que integra o gráfico de A(x) tem inclinação igual a 3 e a do gráfico de B(x) tem inclinação igual a 2. Com base nessas informações e nos gráficos acima, julgue os seguintes itens.

I Caso um cliente queira adquirir menos de 10 CDs, é mais vantajoso para ele comprar na loja B.

II Com R$ 30,00, um cliente compra nas duas lojas a mesma quantidade de CDs.

III Na compra de 15 CDs na loja A, um cliente economizará, em relação à compra na loja B, R$ 0,20 em cada CD.

IV Na compra de 20 CDs na loja B, um cliente economizará, em relação ao que gastaria na compra na loja A, mais de R$ 10,00.

V Com R$ 66,00, um cliente poderá comprar até 18 CDs na loja A, mas não, na loja B.

A quantidade de itens certos é igual a

• A.

  2

• B.

  3

• C.

  4

• D.

  5

X e Y são variáveis aleatórias contínuas com função de densidade de probabilidade conjunta dada por:

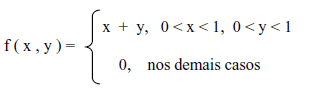
O valor esperado condicional de Y dado x = 1/2 é igual a:

• A.

  1/5;

• B.

  1/2;

• C.

  7/12;

• D.

  3/5;

• E.

  5/6.

A análise fatorial tem como objetivo principal descrever a variabilidade original de um vetor aleatório X com m componentes,

• A. estudando esses m componentes e somando com outros n componentes , mas que sejam ortogonais entre si.
• B. estabelecendo relações de causa e efeito entre esses m componentes.
• C. fazendo uso de um número n (n < m) de variáveis aleatórias, que estejam relacionadas com X através de um modelo linear.
• D. fazendo uso de um número n (n < m) de variáveis aleatórias, chamadas fatores comuns, e que estão relacionadas com X através de um modelo não linear.
• E. tomando uma combinação não linear destes n componentes, onde n < m.

Numa população, 10% das pessoas já tiveram hepatite. Se uma amostra aleatória simples de tamanho 400 for observada, a probabilidade de que ao menos 50 já tenham tido hepatite é aproximadamente de:

• A.

  0,015;

• B.

  0,021;

• C.

  0,032;

• D.

  0,057;

• E.

  0,063.

Uma emissora de televisão promoveu um debate com os 2 candidatos ao segundo turno de uma eleição municipal. Uma pesquisa de opinião deseja avaliar se o debate foi eficaz em mudar a preferência dos eleitores que assistiram ao debate pelos 2 candidatos. Para tanto foram selecionados N adultos aleatoriamente e perguntadas as preferências pelos dois candidatos antes e depois da realização do debate. O teste não paramétrico adequado para avaliar a mudança de preferência é

• A. Teste Wilcoxon-Mann-Whitney.
• B. Teste Exato de Fisher.
• C. Teste de Kruskal Wallis.
• D. Teste de McNemar.
• E. Teste de Komolgorov-Smirnov.

O gráfico abaixo mostra a taxa de desemprego numa determinada região do país em função do tempo no ano de 2006.

• A.

  A taxa de desemprego representa a variável independente desta função.

• B.

  A menor taxa de desemprego foi de, aproximadamente, 16,3% no mês de dezembro.

• C.

  A taxa de desemprego foi estritamente decrescente entre os meses de janeiro e março.

• D.

  A taxa de desemprego teve seu pico em junho de 2006.

• E.

  O tempo (em meses) representa a variável dependente.

O gráfico mostra o faturamento de uma determinada empresa no período de 2000 a 2006, em milhões de reais, e também a previsão do faturamento dessa mesma empresa em 2007.

• A.

  de 2001 a 2006 o faturamento anual teve um crescimento constante.

• B.

  o faturamento em 2001 teve, em relação a 2000, uma queda superior a 50%.

• C.

  em relação ao ano anterior, o faturamento em 2004 teve um crescimento inferior a 30%.

• D.

  a previsão para 2007 corresponde à média aritmética do faturamento dos três anos anteriores.

• E.

  o faturamento em 2005 teve, em relação a 2004, uma queda de 4%.

Uma variável aleatória X tem distribuição binomial com parâmetros n = 25 e p = 1/2. Se usarmos aproximação normal à binomial para calcularmos, com correção de continuidade, P[ 10 < X < 15 ] , obteremos aproximadamente:

• A.

  0,444;

• B.

  0,488;

• C.

  0,532;

• D.

  0,576;

• E.

  0,598.