Questões de Estatística

Considere que X 1 , X 2 , ..., X 100 seja uma amostra aleatória simples de 100 erros de arredondamento. Cada erro de arredondamento é uma variável aleatória contínua uniformemente distribuída no intervalo  . A soma dos elementos dessa amostra é Y = X 1 + X 2 + ... + X 100 , e  é a média amostral. Com base nessas informações, julgue os itens seguintes.

A probabilidade da soma Y ser um valor positivo é igual a 0,5.

• C. Certo
• E. Errado

A quantidade de sólidos totais (Y) na água está relacionada com a sua condutividade elétrica (X), segundo um modelo de regressão linear simples na forma Y = aX + b + E, em que a e b são os coeficientes do modelo e E representa uma variável aleatória normal com média zero e desvio padrão igual a F. Por máxima verossimilhança, o modelo ajustado foi , e as estimativas dos desvios padrões de Y e de X foram, respectivamente, iguais a 800 e 1.000. A condutividade média da água foi igual a 2.000. Com base nessas informações, julgue os itens seguintes.

A razão 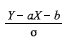 segue uma distribuição normal padrão.

• C. Certo
• E. Errado

Considere que X 1 , X 2 , ..., X 100 seja uma amostra aleatória simples de 100 erros de arredondamento. Cada erro de arredondamento é uma variável aleatória contínua uniformemente distribuída no intervalo  . A soma dos elementos dessa amostra é Y = X 1 + X 2 + ... + X 100 , e  é a média amostral. Com base nessas informações, julgue os itens seguintes.

A probabilidade de se observar  0,65 não é nula.

• C. Certo
• E. Errado

Considere que X 1 , X 2 , ..., X 100 seja uma amostra aleatória simples de 100 erros de arredondamento. Cada erro de arredondamento é uma variável aleatória contínua uniformemente distribuída no intervalo  . A soma dos elementos dessa amostra é Y = X 1 + X 2 + ... + X 100 , e  é a média amostral. Com base nessas informações, julgue os itens seguintes.

A soma Y é uma variável aleatória distribuída segundo uma distribuição normal no intervalo .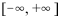

• C. Certo
• E. Errado

Considere que X 1 , X 2 , ..., X 100 seja uma amostra aleatória simples de 100 erros de arredondamento. Cada erro de arredondamento é uma variável aleatória contínua uniformemente distribuída no intervalo  . A soma dos elementos dessa amostra é Y = X 1 + X 2 + ... + X 100 , e  é a média amostral. Com base nessas informações, julgue os itens seguintes.

A probabilidade de ocorrer um evento em que 50% da amostra é formada por valores positivos e a metade restante é formada por valores negativos é igual a 0,5.

• C. Certo
• E. Errado

Um indicador W que mede a qualidade de determinado produto é uma variável aleatória contínua simetricamente distribuída em torno de 7. Tal indicador assume apenas valores positivos e em 75% dos casos seu valor é superior a 3. Com base nessas informações, julgue os itens subseqüentes.

A probabilidade de W ser maior que 14 é igual a zero.

• C. Certo
• E. Errado

A amostra a seguir refere-se a sete tempos de vôo, em horas:

10,0 12,0 8,5 5,0 4,5 3,5 5,5

A média e a mediana desses tempos de vôo valem, respectivamente, em horas:

• A.

  7,0 e 5,0;

• B.

  7,5 e 8,5;

• C.

  7,0 e 5,5;

• D.

  7,5 e 6,0;

• E.

  7,5 e 7,0.

Julgue os itens seguintes acerca de técnicas de amostragem.

Considere que uma amostragem aleatória estratificada seja feita em um universo finito e as unidades amostrais sejam selecionadas sem reposição e com alocação proporcional ao tamanho de cada estrato. Nessa situação, a probabilidade de inclusão de uma unidade amostral é constante, independentemente do estrato em que esta unidade se encontra.

• C. Certo
• E. Errado

O tempo de funcionamento até a ocorrência de falha em uma velha máquina é uma variável aleatória exponencial com média igual a 10 dias. O proprietário da máquina decide colocar a máquina em funcionamento por 30 dias. Considere que o número de falhas segue um processo de Poisson homogêneo. Com base nessas informações, julgue os itens que se seguem.

A probabilidade de a máquina falhar uma vez no período de 30 dias é igual a 3 vezes a probabilidade de a máquina não falhar no período de 30 dias.

• C. Certo
• E. Errado

O tempo de funcionamento até a ocorrência de falha em uma velha máquina é uma variável aleatória exponencial com média igual a 10 dias. O proprietário da máquina decide colocar a máquina em funcionamento por 30 dias. Considere que o número de falhas segue um processo de Poisson homogêneo. Com base nessas informações, julgue os itens que se seguem.

A distribuição do número de falhas é bimodal.

• C. Certo
• E. Errado