Questões de Estatística

O tempo de funcionamento até a ocorrência de falha em uma velha máquina é uma variável aleatória exponencial com média igual a 10 dias. O proprietário da máquina decide colocar a máquina em funcionamento por 30 dias. Considere que o número de falhas segue um processo de Poisson homogêneo. Com base nessas informações, julgue os itens que se seguem.

Dado que a máquina funcionou sem falhar nos primeiros 10 dias, a probabilidade de ela não falhar nos 20 dias seguintes é igual a exp(-2), em que exp(.) representa a função exponencial.

• C. Certo
• E. Errado

Para responder às questões de números 53 a 55, considere o enunciado a seguir.

                 A proporção de pessoas com uma determinada característica numa população é p. Sortearam-se 5 pessoas ao acaso e com reposição dessa população e calculou-se a proporção   de pessoas com a característica na amostra. Desejando-se testar:

H₀: p = 0,5 contra H₁: p = 0,6, com base nesta amostra, decidiu-se rejeitar H₀ se o número de pessoas com a característica na amostra for maior ou igual a 4.

O nível de significância associado ao teste é

• A. 6/64
• B. 5/32
• C. 1/16
• D. 5/64
• E. 6/32

Para responder às questões de números 53 a 55, considere o enunciado a seguir.

                 A proporção de pessoas com uma determinada característica numa população é p. Sortearam-se 5 pessoas ao acaso e com reposição dessa população e calculou-se a proporção   de pessoas com a característica na amostra. Desejando-se testar:

H₀: p = 0,5 contra H₁: p = 0,6, com base nesta amostra, decidiu-se rejeitar H₀ se o número de pessoas com a característica na amostra for maior ou igual a 4.

Se o número observado de pessoas com a característica na amostra foi 5, o nível descritivo associado ao teste é

• A. 5/16
• B. 5/32
• C. 3/16
• D. 1/32
• E. 1/16

Para responder às questões de números 53 a 55, considere o enunciado a seguir.

                 A proporção de pessoas com uma determinada característica numa população é p. Sortearam-se 5 pessoas ao acaso e com reposição dessa população e calculou-se a proporção   de pessoas com a característica na amostra. Desejando-se testar:

H₀: p = 0,5 contra H₁: p = 0,6, com base nesta amostra, decidiu-se rejeitar H₀ se o número de pessoas com a característica na amostra for maior ou igual a 4.

A probabilidade de se rejeitar H₀ quando H₁ é verdadeira é

• A.

  4 × (0,6)⁵

• B.

  (0,6)⁵

• C.

  2,6 × (0,6)⁴

• D.

  1– (0,6)⁵

• E.

  5 × (0,4)(0,6)⁴

Uma variável aleatória X tem distribuição normal com média μ e desvio padrão σ. Desejando-se fazer um teste de hipóteses para a média de X do tipo,

Ho: μ = 120 (σ = 20) contra Ha: μ = 125 (σ = 10),

com base numa amostra de 100 observações, a região crítica apropriada ao teste, dada em termos da média amostral , para que a probabilidade de se cometer erro do tipo I seja a metade da de se cometer erro do tipo II, é dada por

• A.
• B.
• C.
• D.
• E.

O enunciado a seguir refere-se às questões de n^os 67 e 68. Avaliações de terrenos baseiam-se, geralmente, em modelos de regressão linear nos quais o preço de venda é uma função de algumas variáveis tais como o tamanho do terreno, suas condições e localização. Uma amostra de terrenos comercializados no último mês coletou dados sobre o preço da venda, em R$ 1 000,00, o tamanho do terreno, em m2, e a distância ao centro da cidade, em km. Primeiramente obteve-se o modelo com apenas a variável tamanho do terreno, X1, como explicativa do preço de venda. Os principais quantitativos relativos a esse modelo foram calculados como:

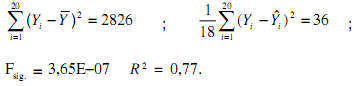
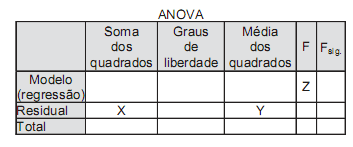
Considerando o quadro acima, os valores de X, Y e Z, respectivamente, são:

• A. 2826, 121 e 3,65E−07
• B. 2178, 121 e 0,77
• C. 2178, 36 e 0,77
• D. 648, 36 e 60,5
• E. 32,4, 18 e 34,1

Para responder às questões de números 68 a 70, considere o enunciado a seguir.

Deseja-se testar a hipótese

A estatística apropriada ao teste

• A.

  tem distribuição Qui-quadrado com 7 graus de liberdade.

• B.

  é baseada num quociente de duas distribuições Quiquadrado, cada uma com 3 graus de liberdade.

• C.

  tem distribuição Qui-quadrado com 6 graus de liberdade.

• D.

  é baseada na diferença  e tem distribuição F de Snedecor com 4 graus de liberdade.

• E.

  tem distribuição F de Snedecor com 4 graus de liberdade no numerador e 4 graus de liberdade no denominador.

Três métodos de ensino diferentes foram aplicados em três grupos distintos de 6 crianças respectivamente. Após o período de aprendizagem experimental foram aplicados testes, e as médias das notas foram utilizadas para avaliar se existe diferença entre os três métodos de ensino. O pesquisador utilizou a técnica de análise de variância para avaliar a diferença entre as médias dos 3 grupos de alunos. Sabendo que o valor da soma de quadrados entre os grupos foi 70, dentro dos grupos foi 1500 e que o valor crítico da distribuição F (com 5% de significância e 2 e 15 graus de liberdade) para este teste foi 3,68, o valor calculado da estatística F e a decisão do teste são

• A. 0,35 e não existe diferença entre as médias.
• B. 1,85 e a média dos três grupos são iguais.
• C. 0,65 e existe pelo menos um grupo com média diferente.
• D. 0,20 e não existe diferença entre as médias.
• E. 4,00 e não existe diferença entre a média dos grupos.

Com base nessas informações, julgue os itens subseqüentes.

O melhor preditor linear de X _n+h é igual a Y(h) X _n .

• C. Certo
• E. Errado

O enunciado a seguir refere-se às questões de n^os 67 e 68. Avaliações de terrenos baseiam-se, geralmente, em modelos de regressão linear nos quais o preço de venda é uma função de algumas variáveis tais como o tamanho do terreno, suas condições e localização. Uma amostra de terrenos comercializados no último mês coletou dados sobre o preço da venda, em R$ 1 000,00, o tamanho do terreno, em m2, e a distância ao centro da cidade, em km. Primeiramente obteve-se o modelo com apenas a variável tamanho do terreno, X1, como explicativa do preço de venda. Os principais quantitativos relativos a esse modelo foram calculados como:

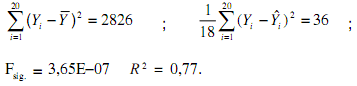
Ao entrar com a variável distância ao centro, o modelo ficou expresso por Yˆ = 9,25 + 2,47 X₁ + 0,78X₂, onde X₁ representa o tamanho do imóvel, em m², e X₂, a distância ao centro, em km. Considerando que todas as variáveis foram testadas e são significativas, analise as afirmações a seguir.

I - Para cada aumento de um metro quadrado no tamanho do terreno, o preço da venda aumenta em 2,47 mil reais, mantendo inalterada a distância ao centro.

II - Para cada aumento de um quilômetro na distância do terreno até o centro, o preço da venda aumenta em 0,78 mil reais, mantendo inalterado o tamanho do terreno.

III - Para um terreno de 40 m², distante do centro 10 km, o preço da venda estimado é de 115,85 mil reais.

É(São) correta(s) a(s) afirmação(ões): (A) I, apenas. (B) II,

• A. I, apenas.
• B. II, apenas.
• C. I e II, apenas.
• D. II e III, apenas.
• E. I, II e III.