Questões de Estatística

Considerando a totalidade das 95 avaliações desse dia, é correto afirmar que a média das notas dista da moda dessas mesmas notas um valor absoluto, aproximadamente, igual a

• A. 0,33.
• B. 0,83.
• C. 0,65.
• D. 0,16.
• E. 0,21.

Seja X uma variável aleatória representando o valor arrecadado de um determinado tributo. Suponha que X tem distribuição normal (população de tamanho infinito) com média %u03BC e desvio padrão de 500 reais. Desejando-se testar

 H0 : %u03BC = 1.000 reais (hipótese nula)

H1 : %u03BC %u2260 1.000 reais (hipótese alternativa)

 tomou-se uma amostra aleatória de 400 valores de X, obtendo-se para a média amostral o valor de 1.060 reais. Seja %u03B1 o nível de significância do teste e suponha que a região de rejeição de H0 é { | Z| > Z _%u03B1/2}, onde Z _%u03B1/2 representa o escore da curva normal padrão tal que P(| Z| > Z _%u03B1/2 ) = %u03B1.

 Tem-se que

• A.

  Se H₀ foi rejeitada, existe um nível de significância β (β > α) tal que H₀ não seria rejeitada.

• B.

  Se H₀ foi rejeitada, existe um nível de significância β (β > α) tal que H₀ não seria rejeitada.

• C.

  H₀ não será rejeitada para Z α/2 < 3.

• D.

  H₀ será rejeitada para Z  a/2 = 2.

• E.

  Para Z α/2 > 2 , H₀ não será rejeitada.

Uma firma distribuidora de eletrodomésticos está interessada em estudar o comportamento de suas contas a receber em dois meses consecutivos. Com este objetivo seleciona, para cada mês, uma amostra de 50 contas. As observações amostrais constam da tabela seguinte:

Assinale a opção que corresponde ao intervalo interquartílico, em reais, para o mês de março.

• A. 3.250,00
• B. 5.000,00
• C. 4.000,00
• D. 6.000,00
• E. 2.000,00

Em um determinado país, deseja-se determinar a relação entre a renda disponível (Y), em bilhões de dólares, e o consumo (C), também em bilhões de dólares. Foi utilizado o modelo linear simples Ci = α + βYi + εi, em que Ci é o consumo no ano i, Yi é o valor da renda disponível no ano i e εi o erro aleatório com as respectivas hipóteses para a regressão linear simples. α e β são parâmetros desconhecidos, cujas estimativas foram obtidas através do método dos mínimos quadrados. Para obtenção desta relação considerou-se ainda as seguintes informações colhidas através da observação nos últimos 10 anos:

Para o cálculo do coeficiente de correlação de Pearson (R), usou-se a fórmula: ) em que Cov(Y,C) é a covariância de Y e C, DP(Y) é o desvio padrão de Y e DP(C) é o desvio padrão de C. Então,

• A. o coeficiente de explicação (R2) correspondente é igual a 64%.
• B. utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-se que, em um ano, caso a renda disponível seja igual a 15 bilhões de dólares, o consumo será igual a 13 bilhões de dólares.
• C. obtendo para um determinado ano uma previsão para o consumo de 10 bilhões de dólares, significa que a renda disponível considerada foi de 12,5 bilhões de dólares.
• D. o valor da estimativa encontrado para o parâmetro β é igual a 0,4.
• E. o valor da estimativa encontrado para o parâmetro α é igual a 10.

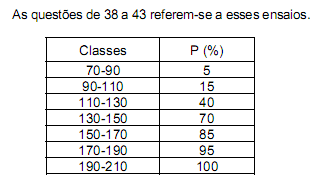
Assinale a opção que corresponde à estimativa do quinto decil da distribuição de X.

• A.

  138,00

• B.

  140,00

• C.

  136,67

• D.

  139,01

• E.

  140,66

No contexto das distribuições de freqüências da Questão 72, as médias amostrais são, respectivamente, R$ 4.920,00 e R$ 4.520,00, para os meses de março e abril. Questiona-se se o valor médio populacional das contas a receber de março difere significantemente do valor médio populacional correspondente de abril. Para verificar esta conjectura, realiza-se um teste de médias, assumindo-se as amostras independentes e provenientes de populações normais com variâncias homogêneas. O valor obtido para a estatística teste foi de 0,78 com valor probabilístico de 43,4%.

Assinale a opção correta.

• A.

  Não há evidência de que as médias sejam distintas no nível de significância de 5% e a estatística teste se distribui como t de Student com 97 graus de liberdade, sob a hipótese da igualdade das médias populacionais.

• B.

  As médias diferem significantemente no nível de 45% e a estatística teste se distribui como t de Student com 97 graus de liberdade, sob a hipótese da igualdade das médias populacionais.

• C.

  Não há evidência de que as médias sejam distintas para qualquer nível α < 43,4% e a estatística teste se distribui como t de Student com 97 graus de liberdade, sob a hipótese da igualdade das médias populacionais.

• D.

  Não há evidência de que as médias difiram no nível de significância de 5% e a estatística teste se distribui como t de Student com 98 graus de liberdade, sob a hipótese da igualdade das médias populacionais.

• E.

  O valor probabilístico associado ao valor da estatística teste não define informação suficiente para que se possa dizer que uma média difere da outra significantemente e a estatística teste se distribui como t de Student com 97 graus de liberdade, sob a hipótese de igualdade das médias populacionais.

O quadro a seguir mostra dados a respeito dos bens X, Y e Z, produzidos por uma empresa fabril hipotética.

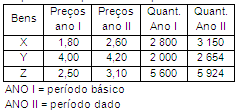
De acordo com o Índice de Preços de Laspeyres, a variação verificada nos preços, entre os anos I e II, foi de:

• A.

  14,10 %

• B.

  15,00 %

• C.

  21,24 %

• D.

  22,19 %

• E.

  39,42 %

A Cia. X presta serviço de manutenção preventiva nos computadores que vende. Em 18 chamadas para realização de serviços de manutenção foram observados os pares (x_i , y_i) onde x_i representa o número de máquinas examinadas na chamada e y_i o tempo gasto, em horas, na visita de inspeção. A tais observações ajusta-se o modelo linear x_i, com o uso de mínimos quadrados ordinários, sob a hipótese de erros com média zero, homoscedásticos, não correlacionados e com os x_i fixos (determinísticos). Foram obtidas as seguintes estatísticas para o ajuste: . As constantes a e b são as estimativas de mínimos quadrados de, respectivamente. Assinale a opção correspondente à estimativa não-viezada da variância residual.

• A. 3,6
• B. 4,7
• C. 1,0
• D. 0,7
• E. 1,2

Para a solução das questões de números 38 a 43 utilize o enunciado que segue.

O atributo do tipo contínuo X, observado como um inteiro, numa amostra de tamanho 100 obtida de uma população de 1000 indivíduos, produziu a tabela de freqüências seguinte:

Assinale a opção que corresponde à estimativa da mediana amostral do atributo X.

• A.

  71,04

• B.

  65,02

• C.

  75,03

• D.

  68,08

• E.

  70,02

Para a solução das questões de números 38 a 43 utilize o enunciado que segue.

O atributo do tipo contínuo X, observado como um inteiro, numa amostra de tamanho 100 obtida de uma população de 1000 indivíduos, produziu a tabela de freqüências seguinte:

Assinale a opção que corresponde à estimativa do número de indivíduos na população com valores do atributo X menores ou iguais a 95,5 e maiores do que 50,5.

• A.

  700

• B.

  638

• C.

  826

• D.

  995

• E.

  900