Questões de Estatística do ano 2006

Sejam X e Y duas variáveis aleatórias e

Tem-se, em qualquer situação:

• A.
• B.
• C.
• D.
• E.

O Teorema de Tchebyshev afirma que no intervalo , tem-se

• A.

  no mínimo 75% dos elementos de uma população qualquer.

• B.

  no máximo 75% dos elementos de uma população, se esta tiver distribuição normal.

• C.

  no máximo 75% dos dados de uma população, se esta tiver distribuição qui-quadrado.

• D.

  exatamente 75% dos dados de uma população qualquer.

• E.

  no máximo 75% dos elementos de uma população qualquer.

Se E₁ e E₂ são dois eventos independentes, então

• A.

  a probabilidade de E₁ é igual à probabilidade de E₂.

• B.

  E₁ e E₂ são mutuamente exclusivos.

• C.

  a probabilidade de E₁ é maior do que a probabilidade de E₂.

• D.

  a probabilidade de E₂ é maior do que a probabilidade de E₁.

• E.

  a ocorrência, ou não, de E₁ não afeta a probabilidade de ocorrência de E₂.

Suzana e Sandra jogam, cada uma, uma moeda. Se do lançamento dessas duas moedas resultar duas caras, Suzana paga a Sandra R$ 6,00. Dando qualquer outro resultado, Sandra paga a Suzana R$ 4,00. Supondo que ambas as moedas sejam estatisticamente honestas, o valor esperado, em reais, dos ganhos de Sandra (considerando- se como ganhos negativos os valores que ela paga à Suzana) é igual a

• A.

  1,5.

• B.

  -0,75.

• C.

  0,75

• D.

  -1,5.

• E.

  2,5.

Um experimento binomial é um experimento que comporta um número fixo de provas independentes, n. Cada prova tem os resultados classificados em apenas duas categorias, a saber: sucesso ou fracasso. Muito embora essa classificação seja arbitrária, costuma-se denotar a probabilidade de sucesso por p, e a probabilidade de fracasso por q. Desse modo, realizando-se 50 provas, a probabilidade de se obter 30 sucessos é dada por

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Ana participou de um concurso e aguarda com ansiedade os resultados das provas que acabou de fazer. Ana estima em 80% a probabilidade de obter conceito A em Estatística, em 40% a probabilidade de obter conceito A em Raciocínio Lógico, e em 36% a probabilidade de obter conceito A em Estatística e Raciocínio Lógico. Hoje, Ana recebeu o resultado da prova de Raciocínio Lógico e verificou que não tirou conceito A. Assim, a probabilidade de Ana também tirar conceito A em Estatística é igual a

• A.

  80 %.

• B. 12 %.
• C.

  60 %.

• D.

  90 %.

• E.

  40 %.

Com a seguinte função de probabilidade conjunta, onde x assume os valores 0 e 1, e y assume os valores, 1, 2 e 3,

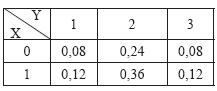
pode-se afirmar que

• A.

  P(Y = 3) = 0,08.

• B.

  P(X =0) = P(Y =2).

• C.

  P(Y = 2 / X = 0) = 0,6.

• D.

  E(X) = 0,4.

• E.

  X e Y são variáveis aleatórias dependentes.

Dois novos tipos de vacina contra determinada doença estão sendo testados: a vacina do tipo A e a vacina do tipo B. Esses dois tipos de vacinas foram aplicados em uma população de voluntários. Sabe-se que 60 % dos voluntários receberam vacina do tipo A e 40% dos voluntários restantes receberam vacina do tipo B. Sabe-se, também, que a vacina do tipo A fornece 70% de imunização e a do tipo B fornece 80% de imunização. Assim, a probabilidade de uma pessoa, escolhida ao acaso, estar imunizada dado que lhe foi aplicada a vacina do tipo A é igual a

• A.

  0,5.

• B.

  0,42.

• C.

  0,68.

• D.

  21/37.

• E.

  42/75.

O Teorema de Bayes diz que, para dois eventos independentes, A e B, com probabilidades não nulas, tem-se que

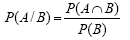
onde, P(A/B) é a probabilidade de ocorrer o evento A, sabendo-se que o evento B já ocorreu. Desse modo pode-se afirmar que

• A.

  se A e B são eventos mutuamente excludentes, então P(A/B) = P(A).

• B.

  se P(B/A) = P(B), então A e B são eventos dependentes.

• C.

  se P(A) ≠ P(B), então A e B são eventos independentes.

• D.

  se P(A) ≠ P(B), então A e B são eventos dependentes.

• E.

  se P(A ∩ B) = 0, então A e B são eventos independentes.

Uma variável aleatória contínua, x, tem função densidade de probabilidade igual a: f(x) = 2x, para 0 < x < 1 e f(x) = 0 para qualquer outro valor de x que estiver fora deste intervalo. Assim, pode-se afirmar que

• A.

  P (0< x < 0,2) = 0,2

• B.

  P (0< x < 0,2) = 0,4

• C.

  P (0< x < 0,2) = 0,24

• D.

  P (0< x < 0,2) = 0,06

• E.

  P (0< x < 0,2) = 0,04