Questões de Estatística do ano 2007

Uma amostra aleatória simples X₁, X₂, ... , X_n, de tamanho n, será obtida de uma população descrita por uma densidade normal com média 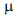 e variância . Se X representa a média amostral e se 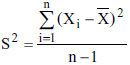  , então a seguinte variável tem distribuição qui-quadrado com n – 1 graus de liberdade:

• A.

  S²

• B.
• C.
• D.
• E. nS²

Para testar se as proporções populacionais referentes à classificação dos elementos populacionais em quatro categorias A, B, C e D são iguais a 20%, 30%, 30% e 20%, uma amostra aleatória simples de tamanho 400 foi obtida e as freqüências observadas foram: classe A: 80, classe B: 100, classe C: 120, classe D: 100. O valor da estatística qui-quadrado usual para esses dados é aproximadamente igual a:

• A.

  2,64;

• B.

  4,06;

• C.

  5,28;

• D.

  6,78;

• E.

  8,33.

Com o objetivo de se testar independência entre dois atributos, a tabela de contingências 3 X 2 a seguir foi observada:

A freqüência esperada sob a hipótese de independência na célula ( 2, 2 ) é igual a:

• A.

  320;

• B.

  360;

• C.

  440;

• D.

  460;

• E.

  520.

Um dos critérios para a avaliação da qualidade da água para o consumo humano é a detecção de coliformes fecais na água distribuída à população. A tabela acima apresenta os resultados das análises de 5.600 amostras de água coletadas, entre os anos de 1995 a 2000, em uma grande cidade, conforme as estações do ano.

Considerando as informações da tabela acima, julgue os itens a seguir.

O valor da estatística quiquadrado com respeito à hipótese de independência entre os resultados e as estações do ano é superior a 15.

• C. Certo
• E. Errado

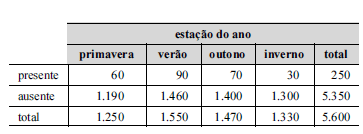
Um dos critérios para a avaliação da qualidade da água para o consumo humano é a detecção de coliformes fecais na água distribuída à população. A tabela acima apresenta os resultados das análises de 5.600 amostras de água coletadas, entre os anos de 1995 a 2000, em uma grande cidade, conforme as estações do ano.

Considerando as informações da tabela acima, julgue os itens a seguir.

Considere que uma nova amostra seja retirada em algum instante do ano, e o resultado da análise acuse ausência de coliformes fecais. Nessa situação, pelo princípio da máxima verossimilhança, é correto inferir que essa amostra tenha sido retirada no verão.

• C. Certo
• E. Errado

Uma pesquisa produziu a tabela de contingência a seguir para duas variáveis qualitativas A e B.

Considerando-se o teste de homogeneidade para essa tabela, a estatística qui-quadrado é igual a

• A.

  

• B.

  

• C.

  

• D.

  

Um levantamento estatístico ouviu a opinião da satisfação dos consumidores acerca de determinado produto. De uma amostra aleatória de 500 consumidores, observou-se que 100 pessoas eram usuárias do produto fornecido pelo fabricante A, e as 400 restantes eram usuárias do produto do fabricante B. Entre os primeiros usuários, 70 estavam satisfeitos com o produto fornecido pelo fabricante A. Por outro lado, o estudo mostrou que 120 usuários do produto do fabricante B não estavam satisfeitos na ocasião do levantamento. Com base nessas informações, julgue os itens seguintes.

A estatística qui-quadrado do teste de homogeneidade é inferior a 0,81.

• C. Certo
• E. Errado

O fabricante de uma balança de precisão afirma que o desvio padrão das medições dessa balança é de 0,0002 g. Considere que um usuário dessa balança faça um experimento para testar a afirmação do fabricante. Após 8 medições, esse usuário verifica que o desvio padrão amostral foi igual a 0,0005 g. O usuário decide testar a hipótese nula  versus a hipótese alternativa  . Com base nessas informações, julgue os itens a seguir.

A estatística qui-quadrado para o teste em questão é inferior a 40.

• C. Certo
• E. Errado

 

Considere que  a vazão V de um oleoduto seja uma variável aleatória que siga uma distribuição normal com média igual a 1.000 m 3 por dia e desvio-padrão igual a 500 m 3 por dia. Nessa situação, julgue os itens subseqüentes.

A probabilidade de V ser igual a 1.000 m ³ por dia é superior a 0,01.

• C. Certo
• E. Errado

Para responder às questões de números 51 e 52, considere o enunciado a seguir.

                    Seja (X,Y) uma amostra aleatória simples, com reposição, de uma distribuição normal com média μ e variância 1. Considere os estimadores L, M, e N de μ dados a seguir:

                    L = 2/3X + 1/3Y; M = 1/4X + 3/4Y; N = 1/2X + 1/2Y.

É verdade que

• A.

  apenas N é não viciado.

• B.

  os três são não viciados e o de menor variância é o M.

• C.

  os três são não viciados e o de menor variância é o N.

• D.

  L é viciado, mas é o de menor variância.

• E.

  os estimadores L e M são não viciados e suas variâncias são iguais.