Questões de Estatística do ano 2010

Considerando um espaço amostral 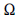 gerado por um experimento aleatório g e os eventos aleatórios A₁, A₂, ... contidos em 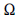, julgue os itens que se seguem acerca da definição axiomática de probabilidade e seus resultados básicos.

• C. Certo
• E. Errado

Considerando um espaço amostral 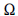 gerado por um experimento aleatório g e os eventos aleatórios A₁, A₂, ... contidos em 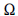, julgue os itens que se seguem acerca da definição axiomática de probabilidade e seus resultados básicos.

• C. Certo
• E. Errado

Considerando um espaço amostral 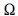 gerado por um experimento aleatório g e os eventos aleatórios A₁, A₂, ... contidos em 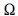, julgue os itens que se seguem acerca da definição axiomática de probabilidade e seus resultados básicos.

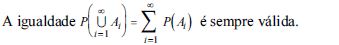
• C. Certo
• E. Errado

A probabilidade de haver atraso na entrega de um pedido de uma diligência investigatória é igual a 0,20. Se esse atraso se concretizar, a probabilidade de ocorrer atraso no início dessa diligência é igual a 0,25. Mas, caso não haja atraso nessa entrega, a probabilidade de ocorrer atraso no início dessa diligência passa a ser igual a 0,15.

Com base nessas informações, a partir dos eventos A = atraso na entrega de um pedido de uma diligência investigatória e B = atraso no início da diligência. julgue os próximos itens.

A probabilidade de ocorrer o evento A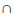  B é inferior a 10%.

• C. Certo
• E. Errado

A probabilidade de haver atraso na entrega de um pedido de uma diligência investigatória é igual a 0,20. Se esse atraso se concretizar, a probabilidade de ocorrer atraso no início dessa diligência é igual a 0,25. Mas, caso não haja atraso nessa entrega, a probabilidade de ocorrer atraso no início dessa diligência passa a ser igual a 0,15.

Com base nessas informações, a partir dos eventos A = atraso na entrega de um pedido de uma diligência investigatória e B = atraso no início da diligência. julgue os próximos itens.

A probabilidade de ocorrer o evento A é superior a 20%.

• C. Certo
• E. Errado

A probabilidade de haver atraso na entrega de um pedido de uma diligência investigatória é igual a 0,20. Se esse atraso se concretizar, a probabilidade de ocorrer atraso no início dessa diligência é igual a 0,25. Mas, caso não haja atraso nessa entrega, a probabilidade de ocorrer atraso no início dessa diligência passa a ser igual a 0,15.

Com base nessas informações, a partir dos eventos A = atraso na entrega de um pedido de uma diligência investigatória e B = atraso no início da diligência. julgue os próximos itens.

Se houve atraso no início da diligência, a probabilidade de não ter havido atraso na entrega do pedido da diligência é superior a 50%.

• C. Certo
• E. Errado

A probabilidade de haver atraso na entrega de um pedido de uma diligência investigatória é igual a 0,20. Se esse atraso se concretizar, a probabilidade de ocorrer atraso no início dessa diligência é igual a 0,25. Mas, caso não haja atraso nessa entrega, a probabilidade de ocorrer atraso no início dessa diligência passa a ser igual a 0,15.

Com base nessas informações, a partir dos eventos A = atraso na entrega de um pedido de uma diligência investigatória e B = atraso no início da diligência. julgue os próximos itens.

Os eventos A e B não são independentes.

• C. Certo
• E. Errado

Uma empresa possui um serviço de atendimento ao consumidor (SAC). Diariamente, um atendente registra, em uma folha de papel, as chamadas recebidas. Cada folha de registro do atendente do SAC permite o registro de até 20 chamadas. O atendente efetua os registros de forma sequencial, anotando, para cada chamada, se houve reclamação. De acordo com os dados históricos, sabe-se que, a cada 20 chamadas, a probabilidade de se registrar exatamente uma reclamação é constante e igual a 0,05. Sabe-se também que o número médio diário de reclamações registradas pelo SAC é igual a 1.

Com base nessas informações e considerando 2,71 como valor aproximado para o número e, base do logaritmo natural, julgue os itens de 83 a 86.

Suponha que o número diário de reclamações registradas pelo SAC siga uma distribuição de Poisson. Nessa situação, a probabilidade de haver o registro de, no máximo, uma reclamação em determinado dia é superior a 67%.

• C. Certo
• E. Errado

Uma empresa possui um serviço de atendimento ao consumidor (SAC). Diariamente, um atendente registra, em uma folha de papel, as chamadas recebidas. Cada folha de registro do atendente do SAC permite o registro de até 20 chamadas. O atendente efetua os registros de forma sequencial, anotando, para cada chamada, se houve reclamação. De acordo com os dados históricos, sabe-se que, a cada 20 chamadas, a probabilidade de se registrar exatamente uma reclamação é constante e igual a 0,05. Sabe-se também que o número médio diário de reclamações registradas pelo SAC é igual a 1.

Com base nessas informações e considerando 2,71 como valor aproximado para o número e, base do logaritmo natural, julgue os itens de 83 a 86.

O modelo probabilístico mais adequado para representar a distribuição do número de reclamações por folha de registro é a distribuição binomial negativa.

• C. Certo
• E. Errado

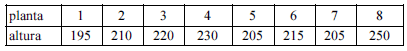
Considerando a situação apresentada no texto, que n = 8 e que a tabela acima apresenta as alturas registradas (em cm) no décimo mês das plantas monitoradas, julgue os próximos itens.

Se a hipótese H₀ for válida, então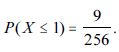

• C. Certo
• E. Errado