Questões de Estatística do ano 2010

O processo não possui limite estacionário se p =1 e q =1.

• C. Certo
• E. Errado

O passeio aleatório simples não é uma cadeia de Markov.

• C. Certo
• E. Errado

No passo 1 (n =1), o passeio aleatório pode assumir valor -1 ou 1. Logo, nos passos pares 2n, esse processo assume valor par (inclusive o valor zero) com probabilidade 1; nos passos ímpares 2n + 1, esse mesmo processo assume valor ímpar com probabilidade 1.

• C. Certo
• E. Errado

Determinada fábrica produz certo tipo de peça. As peças produzidas são remetidas aos consumidores em lotes de tamanho N, mas é possível que esses lotes contenham peças defeituosas. Um cliente, para avaliar a qualidade das peças de certo lote, efetua uma amostragem aleatória simples sem reposição de tamanho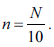

Com base nessas informações, e considerando que o lote examinado pelo cliente possui exatamente 4% de peças defeituosas, julgue o item subsequente.

Se N = 100, a probabilidade de não haver peças defeituosas na amostra será inferior a 0,3.

• C. Certo
• E. Errado

Considere que a variável aleatória X possa assumir n valores diferentes com probabilidades p₁, p₂, ..., p_n, respectivamente, em que n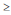 2. A respeito das expressões das entropias de ordem q de Shannon e de Rényi associadas a X, e sabendo que ambas utilizam o logaritmo neperiano, julgue os itens a seguir.

Se todas as probabilidades p_i (i = 1,.., n) forem iguais, então a entropia de Shannon e a entropia de Renyi serão iguais a ln(n), para qualquer valor de q.

• C. Certo
• E. Errado

Considere que a variável aleatória X possa assumir n valores diferentes com probabilidades p₁, p₂, ..., p_n, respectivamente, em que n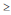 2. A respeito das expressões das entropias de ordem q de Shannon e de Rényi associadas a X, e sabendo que ambas utilizam o logaritmo neperiano, julgue os itens a seguir.

Nessas condições, a entropia de Renyi será igual à de Shannon sempre que q for um número inteiro positivo.

• C. Certo
• E. Errado

Considere que a quantidade de processos que chegam a um auditor diariamente siga uma distribuição de Poisson, com parâmetro 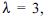, e que cada processo, independentemente dos demais, tenha probabilidade 0,2 de incorrer em algum tipo de irregularidade. Com base nessa situação, julgue os itens que se seguem.

Em face dessa situação, é correto afirmar que o número esperado de processos com irregularidade que o auditor recebe a cada dia é igual a 0,5.

• C. Certo
• E. Errado

Considere que a quantidade de processos que chegam a um auditor diariamente siga uma distribuição de Poisson, com parâmetro 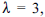, e que cada processo, independentemente dos demais, tenha probabilidade 0,2 de incorrer em algum tipo de irregularidade. Com base nessa situação, julgue os itens que se seguem.

Caso o auditor seja capaz de avaliar, no máximo, quatro processos por dia, então, o número esperado de processos avaliados por ele será inferior a três.

• C. Certo
• E. Errado

Cinquenta prisioneiros de uma ala são numerados de 1 a 50. O guarda chama aleatoriamente, após sorteio, um prisioneiro e vê que o número dele é múltiplo de 4 e de 6. O prisioneiro retorna à ala de detentos, e novamente o guarda chama aleatoriamente (por sorteio) um prisioneiro. Qual é a probabilidade de o número desse prisioneiro ser, agora, um múltiplo de 4 ou de 6?

• A.

  7/25

• B.

  8/25

• C.

  13/50

• D.

  17/50

• E.

  14/25

Considere que a duração do tempo de uso de lâmpadas fluorescentes seja aproximadamente normal. O modelo M₁ de uma lâmpada fluorescente tem duração média de 6.000 h, enquanto o modelo M₂ tem duração média de 8.000 h, e ambos os modelos apresentam variância de 245.000 h². Assinale a alternativa que apresenta a probabilidade de uma lâmpada do modelo M1 durar mais do que uma do M₂.

• A.

  0,21%

• B.

  0,82%

• C.

  2,28%

• D.

  2,86%

• E.

  4,77%