Questões de Estatística do ano 2011

Seja X uma variável aleatória normalmente distribuída com média μ e variância populacional desconhecida. Deseja-se testar a hipótese em que a média μ da população, considerada de tamanho infinito, é superior a 20, ao nível de significância de 5%. Para testar a hipótese, foi extraída uma amostra aleatória de 9 elementos, apurando-se uma média igual a 21 e com a soma dos quadrados destes elementos igual a 3.987. As hipóteses formuladas foram H0: μ = 20 (hipótese nula) e H1: μ > 20 (hipótese alternativa). Utilizando o teste t de Student, obtém-se que o valor da estatística tc (t calculado), para ser comparado com o t tabelado, é igual a

• A.

  1,5.

• B.

  2,0.

• C.

  2,5.

• D.

  3,0.

• E.

  4,0.

Em um período, é realizada uma pesquisa com 150 passageiros escolhidos aleatoriamente em um grande aeroporto, detectandose que 60 deles são do sexo feminino. Com base nesta pesquisa, deseja-se testar a hipótese de que a proporção dos passageiros do sexo feminino é igual a dos passageiros do sexo masculino. Sendo p a proporção dos passageiros do sexo feminino, foram formuladas as hipóteses H0: p = 0,50 (hipótese nula) e H1: p ≠ 0,50 (hipótese alternativa), supondo normal a distribuição da frequência relativa dos passageiros do sexo feminino. Utilizando as informações da distribuição normal padrão (Z), em que as probabilidades P(Z > 1,96) = 2,5% e P(Z > 2,58) = 0,5%, é correto afirmar que H0

• A.

  não é rejeitada ao nível de significância de 5%.

• B.

  é rejeitada para qualquer nível de significância inferior a 5%.

• C.

  é rejeitada tanto ao nível de significância de 1% como de 5%.

• D.

  não é rejeitada para qualquer nível de significância inferior a 1%.

• E.

  é rejeitada para qualquer nível de significância superior a 1% e inferior a 5%.

• A.

  1 < r  2.

• B.

  2 < r  3.

• C.

  3 < r  4.

• D.

  4 < r  5.

• E.

  r > 5.

Atenção: Para resolver as questões de números 55 a 57, dentre informações dadas abaixo, utilize aquelas que julgar apropriadas. Se Z tem distribuição normal padrão, então: P(Z<0,5) = 0,691; P(Z < 1) = 0,841; P(Z<1,5) = 0,933; P(Z<2) = 0,977; P(Z<2,58) = 0,995.

Uma metalúrgica produz blocos cilíndricos cujo diâmetro é uma variável aleatória X, com distribuição normal, média μ = 60 mm e desvio padrão σ = 9 mm. Os diâmetros de uma amostra de 9 blocos são medidos a cada hora, e a média da amostra é usada para decidir se o processo de fabricação está dentro dos padrões de qualidade exigidos. A regra de decisão envolvida no procedimento de qualidade é a seguinte: Se o diâmetro médio da amostra de 9 cilindros for superior a 64,5 mm ou inferior a 54 mm, o processo deve ser interrompido para ajustes; caso contrário o processo de fabricação continua. A probabilidade do processo parar desnecessariamente (isto é, parar quando a média μ e o desvio padrão σ permanecem sendo os valores acima citados) é de

• A.

  13,4%.

• B.

  12%.

• C.

  11,2%.

• D.

  10%.

• E.

  9%.

Com base na amostra observada, adotando-se um nível de significância de 5%, não há evidências estatísticas que permitem rejeitar a hipótese nula.

• C. Certo
• E. Errado

• C. Certo
• E. Errado

O valor da estatística do teste foi superior a 3 e inferior a 4.

• C. Certo
• E. Errado

• A.

  

• B.
• C.

  

• D.

  

• E.

  

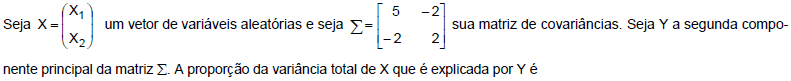
• A.

  6/7.

• B.

  1/7.

• C.

  1/6.

• D.

  3/7.

• E.

  2/7.

Considerando que X, Y e Z sejam variáveis aleatórias, que a seja uma constante não nula e que E, Md, Var, Cov, Q₁ e Q₃ denotem, respectivamente, esperança, mediana, variância, covariância, primeiro quartil e terceiro quartil, julgue os itens a seguir.

Var(X – Y) = Var(X) – Var(Y) + 2Cov(X Y).

• C. Certo
• E. Errado