Questões de Estatística do ano 2011

A respeito das medidas de assimetria e curtose, julgue os próximos itens.

Entre as distribuições A e B a seguir, aquela que melhor representa uma distribuição com assimetria negativa e curtose positiva é a distribuição A.

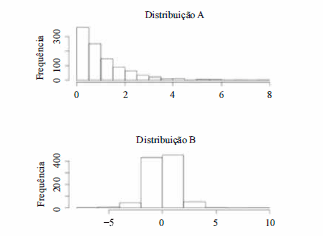
• C. Certo
• E. Errado

A respeito das medidas de assimetria e curtose, julgue os próximos itens.

A curtose de uma distribuição correspondente a um conjunto de dados X com n elementos e média aritmetica  pode ser , corretamente calculada a partir da expressão abaixo. No caso em que X tem distribuição normal, a curtose é zero.

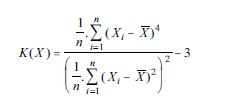
• C. Certo
• E. Errado

Considerando o gráfico acima e o fato de os pontos indicarem uma única observação, julgue os itens que se seguem, referentes ao coeficiente de assimetria.

Entre os grupos B, C e D, o que tem o menor coeficiente de assimetria é o grupo D.

• C. Certo
• E. Errado

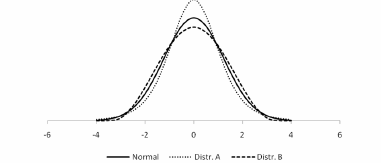
O gráfico acima mostra a função de densidade de uma distribuição normal e de duas outras distribuições A e B. No que se refere a esse gráfico, julgue os itens que se seguem.

A curtose da distribuição A é superior às curtoses das outras duas distribuições.

• C. Certo
• E. Errado

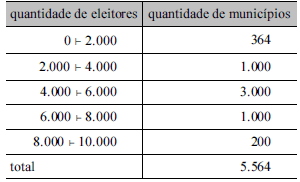
A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.

A curtose da distribuição em questão pode ser avaliada com base na estimativa do quarto momento central, a qual deve ser comparada com o valor de referência 3, visto que todas as distribuições simétricas possuem quarto momento central igual a 3.

• C. Certo
• E. Errado

O coeficiente de curtose é inferior a 0,25.

• C. Certo
• E. Errado

A população correspondente aos salários dos empregados de um determinado ramo de atividade é considerada normal, de tamanho infinito e desvio padrão populacional igual a R$ 400,00. Uma amostra aleatória de tamanho 100 é extraída desta população obtendo-se uma média igual a R$ 2.050,00. Com base nesta amostra, deseja-se testar a hipótese se a média μ da população é igual a R$ 2.000,00, a um nível de significância de 5%. Foram formuladas as hipóteses Ho: μ = R$ 2.000,00 (hipótese nula) e H1: μ ≠ R$ 2.000,00 (hipótese alternativa). Para a tomada de decisão, o valor do escore reduzido, utilizado para comparação com o valor z da distribuição normal padrão (Z) tal que a probabilidade P (|Z| > z) = 5%, é

• A.

  2,50.

• B.

  2,25.

• C.

  2,00.

• D.

  1,75.

• E.

  1,25.

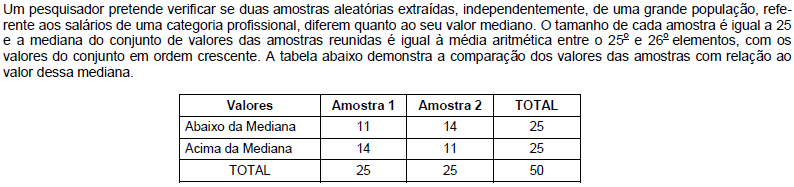
O pesquisador utilizou o teste da mediana para decidir se as medianas das duas amostras são iguais, ao nível de significância de 5%. As hipóteses formuladas foram H_o: As medianas são iguais (hipótese nula) e H₁: As medianas são diferentes (hipótese alternativa), sabendo que ao nível de significância de 5% a variável qui-quadrado com 1 grau de liberdade é igual a 3,84. Então, uma conclusão correta é que H_o

• A.

  não é rejeitada e o qui-quadrado observado é igual a 0,36.

• B.

  é rejeitada e o qui-quadrado observado é igual a 0,36.

• C.

  não é rejeitada e o qui-quadrado observado é igual a 0,72.

• D.

  é rejeitada e o qui-quadrado observado é igual a 0,72.

• E.

  não é rejeitada e o qui-quadrado observado é igual a 1,96.

Assinale a alternativa correta a respeito da Teoria da Decisão Estatística, dos testes de hipóteses e significância, assim como dos erros do tipo I e do tipo II.

• A.

  Se uma hipótese for rejeitada quando deveria ser aceita, diz-se que foi cometido um erro do tipo II.

• B.

  Para que quaisquer testes de hipótese ou regras de decisão sejam bons, eles devem ser planejados de modo que os erros de decisão sejam reduzidos ao mínimo.

• C.

  Se uma hipótese for aceita quando deveria ser rejeitada, diz-se que foi cometido um erro do tipo I.

• D.

  Qualquer hipótese que difira de uma prefixada é denominada hipótese estatística.

• E.

  Ao se tentar chegar às decisões, é conveniente a formulação de hipóteses ou de conjecturas acerca das populações interessadas, cujas suposições podem ser ou não verdadeiras e são denominadas hipóteses alternativas.

Elabora-se um teste estatístico com a hipótese nula, H₀, de que determinada moeda seja honesta, isto é, se for lançada, a probabilidade de o resultado ser cara é 50% e de ser coroa também é 50%. A hipótese alternativa é de que a moeda seja desonesta. O procedimento do teste consiste em lançá-la cinco vezes; se o resultado for cinco caras ou cinco coroas H₀ será rejeitada.

A probabilidade de se cometer um erro do tipo I é

• A.

  1/8

• B.

  1/16

• C.

  1/32

• D.

  1/64

• E.

  1/128