Questões de Estatística do ano 2011

Considerando um modelo de regressão linear com intercepto b₀ e três variáveis regressoras cujos respectivos coeficientes são b₁, b₂ e b₃, julgue os itens subsequentes.

Para se testar a hipótese nula H₀: b₁ = b₂, o teste F é feito comparando-se a soma de quadrados dos resíduos do modelo completo com a soma de quadrados dos resíduos do modelo restrito à hipótese b₁ = b₂.

• C. Certo
• E. Errado

Com relação aos testes de hipóteses paramétricos, julgue os itens subsecutivos.

Define-se poder do teste como a probabilidade de a hipótese nula ser rejeitada quando esta é, de fato, falsa. Logo, o poder do teste é igual a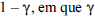  é a probabilidade de haver o erro do tipo I.

• C. Certo
• E. Errado

Com relação aos testes de hipóteses paramétricos, julgue os itens subsecutivos.

Considere que duas amostras independentes, de tamanhos n₁ > 1 e n₂ > 1, em que n₁ + n₂ < 30, foram retiradas de duas populações normais com variâncias desconhecidas e diferentes. Nessa situação, é correto afirmar que a estatística do teste dada pela diferença padronizada das médias aritméticas dessas duas amostras segue, sob a hipótese nula, distribuição t de Student com n₁ + n₂ – 2 graus de liberdade.

• C. Certo
• E. Errado

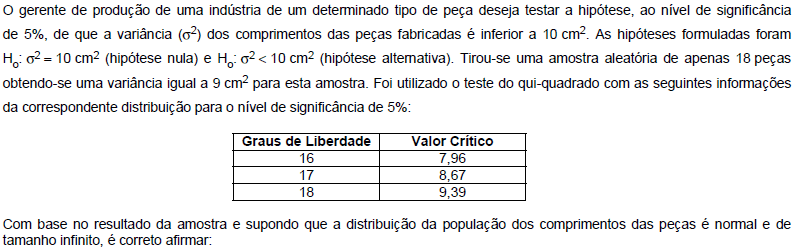
• A.

  ao nível de significância de 5%, a variância é inferior a 10 cm².

• B.

  o valor do qui-quadrado observado para comparação com o qui-quadrado tabelado é superior a 8,67 e inferior a 9,39.

• C.

  para qualquer nível de significância, a conclusão é que a variância populacional é inferior a 10 cm².

• D.

  o número de graus de liberdade aplicado ao teste é igual a 16.

• E.

  para qualquer nível de significância inferior a 5% a conclusão é de que a variância dos comprimentos das peças não é inferior a 10 cm².

A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

• C. Certo
• E. Errado

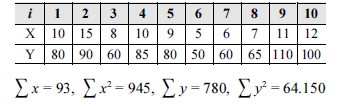
A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

• C. Certo
• E. Errado

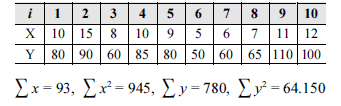
A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

Considere um teste de hipóteses acerca da média da variável X. Nesse caso, se todos os demais momentos da distribuição X forem desconhecidos, então a estatística apropriada para esse teste segue uma distribuição t com 9 graus de liberdade.

• C. Certo
• E. Errado

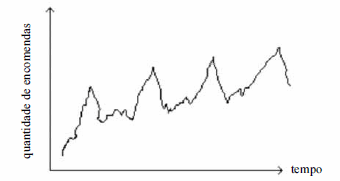
O gráfico acima mostra a evolução temporal da quantidade mensal de encomendas X entregues em determinada cidade. A partir dessa figura e dos conceitos de séries temporais, julgue os itens subsequentes.

Uma das suposições do modelo AR(p) é que os erros aleatórios sejam ruído branco.

• C. Certo
• E. Errado

Acerca de inferência estatística, julgue os itens de 75 a 85.

Suponha que se deseje testar H0 : θ = θ0 versus H1 : θ ≠ θ0, em que θ é um parâmetro populacional desconhecido e θ0 ∈ [φ1, φ2], em que [φ1, φ2] representa o intervalo de (1 – ") × 100% de confiança para θ. Nessa situação, se o nível de significância do teste for igual a " × 100%, a hipótese nula do teste em questão não será rejeitada.

• C. Certo
• E. Errado

A proporção de pessoas favoráveis a certo projeto governamental, em uma população, é p. Sorteiam-se 4 pessoas ao acaso e com reposição desta população e calcula-se a proporção pˆ de pessoas na amostra favoráveis ao projeto. Desejando-se testar H0: p = 0,5 versus H1: p = 0,7, decidiu-se rejeitar a hipótese nula se a região crítica do teste relativa a pˆ for {1}. Nessas condições, a probabilidade do erro do tipo II é

• A.

  0,7599

• B.

  0,7012

• C.

  0,5035

• D.

  0,3240

• E.

  0,2835