Questões sobre Medidas de Dispersão
Lista completa de Questões sobre Medidas de Dispersão para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Considere uma amostra aleatória simples X1, X2, ..., Xn de uma distribuição exponencial com média
. O estimador não viesado de variância uniformemente mínima de 
é:
- A.
- B.
- C.
- D.
- E.
- A.
4,53.
- B.
9,92.
- C.
10,31.
- D.
11,21.
- E.
40,90.
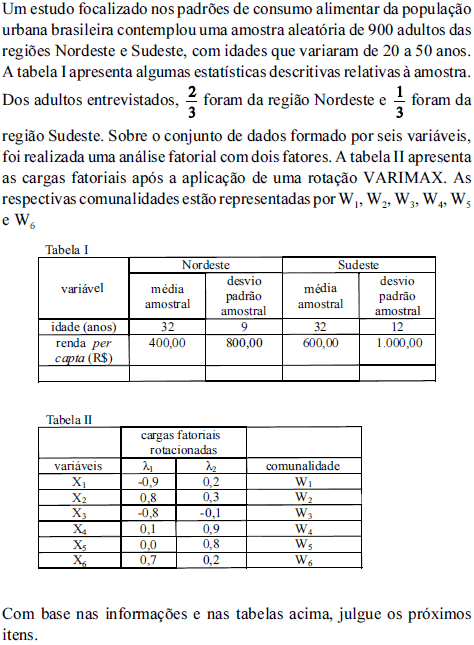
O percentual da variação total explicada pelos dois fatores é superior a 65% da variação total.
- C. Certo
- E. Errado
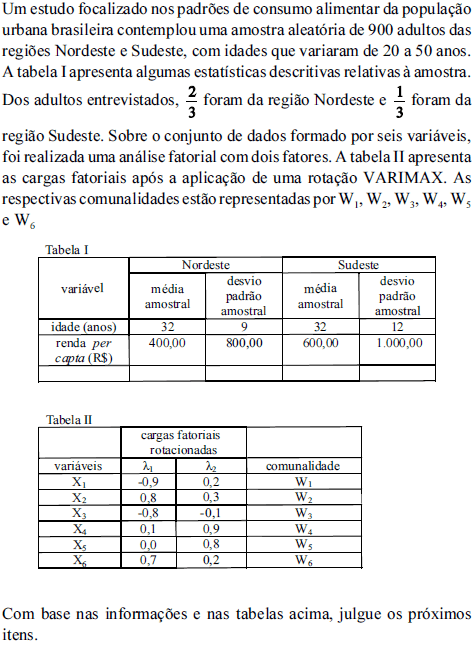
A variação devida ao primeiro fator é inferior a 3.
- C. Certo
- E. Errado
A tabela a seguir apresenta algumas estatísticas das notas dos alunos de determinado curso que participaram do ENADE 2005.
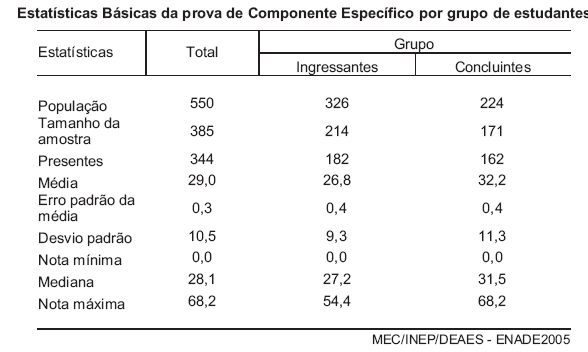
Com base na tabela acima, pode-se afirmar que a(s)
I - menor dispersão das notas ocorre no grupo dos alunos concluintes;
II - amplitude total das notas é menor no grupo dos concluintes;
III - variância das notas é menor no grupo de ingressantes;
IV - medidas de posição na distribuição de notas são menores no grupo dos ingressantes.
São verdadeiras APENAS as afirmações
- A. I e III
- B. I e IV
- C. II e III
- D. II e IV
- E. III e IV
Quais dentre as relacionadas nas alternativas abaixo podem ser consideradas medidas de dispersão ou da variabilidade estatística:
- A. Quartis decis percentis e desvio médio.
- B. Percentis amplitude parcial variância e desvio padrão.
- C. Desvio padrão amplitude total variância e desvio médio.
- D. Percentis coeficiente de Pearson variância e desvio padrão.
Considere que X1, X2, ..., Xn seja uma amostra aleatória simples de uma distribuição X, cuja função de densidade é dada por para 
para x < 0 ou x >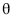 
em que 
> 0. Com base nessas informações, julgue os itens a seguir. A distribuição amostral do 3.º quartil da amostra aleatória X1, X2, ..., Xn é assintoticamente normal, com média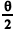 
e variância 
- C. Certo
- E. Errado
NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.
Observa-se que a média de idade é um indicador central, porém, percebe-se que houve variabilidade entre as idades dos criminosos. Portanto, relativamente, esta variabilidade pode ser considerada como sendo:
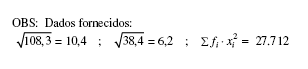
- A.
baixa
- B.
média
- C.
normal
- D.
alta
Estatística - Medidas de Dispersão - Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP) - 2007
Considere os histogramas a seguir, correspondentes às distribuições das variáveis X e Y.
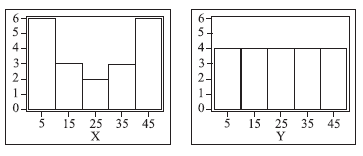
Pode-se afirmar que
- A.
a variância de Y é menor que a variância de X.
- B.
a mediana de Y é maior que a de X.
- C.
não é possível comparar as variâncias com as informações disponíveis.
- D.
as duas variáveis têm o mesmo desvio padrão.
- E.
a média de X é maior do que a média de Y.
O desvio padrão, a média e a moda, respectivamente, são medidas de:
- A.
dispersão, tendência e dispersão.
- B.
dispersão, tendência e tendência.
- C.
tendência, dispersão e tendência.
- D.
tendência, tendência e dispersão.
- E.
tendência, dispersão e dispersão.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
