Questões sobre Probabilidade

Dado um conjunto finito ��, chamamos de conjunto das partes de ��ou 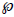��) ao conjunto cujos elementos são todos os subconjuntos de ��. Com base nesta definição, é CORRETO afirmar que

• A.

  ∅é elemento de  �� , se, e somente se for elemento também de ��.

• B.

  ∅é elemento de  �� , qualquer que seja o conjunto ��.

• C.

  {∅}é elemento de ��, ) se, e somente se, for elemento também do conjunto ��.

• D.

  {∅}jamais pode ser elemento de  �� , pois �� é assumido como conjunto finito.

• E.

  Se �� ≠ ∅, então {∅} é elemento de (��)

Considere que a chegada e o atendimento de estudantes em determinada fila para matrícula em uma escola possam ser modelados segundo um passeio aleatório simples em tempo discreto t = 0, 1, 2, 3 ... e que, em cada instante t, apenas dois eventos sejam possíveis: ou um novo estudante entra na fila com probabilidade p ou um estudante na fila é atendido com probabilidade 1 - p. Suponha, ainda, que, no instante inicial t = 0, a quantidade de estudantes na fila não seja nula e grande o suficiente para que a fila não fique vazia em pouco tempo, e que, a cada instante t, no máximo um estudante pode ser atendido.

Com base nessa situação, julgue os itens a seguir.

A fila somente atinge seu tamanho original em instantes de tempo t que são múltiplos de 2.

• C. Certo
• E. Errado

Com respeito a distribuições conjuntas (X,Y), julgue os itens de 117 a 120.

• C. Certo
• E. Errado

Com respeito a distribuições conjuntas (X,Y), julgue os itens de 117 a 120.

• C. Certo
• E. Errado

Estimou-se que, na região Norte do Brasil, em 2009, havia 1.074.700 analfabetos com 15 anos de idade ou mais, em uma população total de, aproximadamente, 10.747.000 habitantes, e que na região Centro-Oeste, no mesmo ano, havia 840.433 analfabetos com 15 anos de idade ou mais, em uma população total de, aproximadamente, 10.505.415 habitantes. A partir dessas informações, julgue o item subsequente.

A probabilidade de uma pessoa com 15 anos de idade ou mais escolhida ao acaso em 2009, na região Norte ou na região Centro-Oeste, ser analfabeta é inferior a 20%.

• C. Certo
• E. Errado

Considerando que, em uma concessionária de veículos, tenha sido verificado que a probabilidade de um comprador adquirir um carro de cor metálica é 1,8 vez maior que a de adquirir um carro de cor sólida e sabendo que, em determinado período, dois carros foram comprados, nessa concessionária, de forma independente, julgue os itens a seguir.

A probabilidade de que ao menos um dos dois carros comprados seja de cor sólida é igual a 460/784.

• C. Certo
• E. Errado

Considerando que, em uma concessionária de veículos, tenha sido verificado que a probabilidade de um comprador adquirir um carro de cor metálica é 1,8 vez maior que a de adquirir um carro de cor sólida e sabendo que, em determinado período, dois carros foram comprados, nessa concessionária, de forma independente, julgue os itens a seguir.

A probabilidade de que os dois carros comprados sejam de cor metálica é 3,24 vezes maior que a probabilidade de que eles sejam de cor sólida.

• C. Certo
• E. Errado

Considerando que, em uma concessionária de veículos, tenha sido verificado que a probabilidade de um comprador adquirir um carro de cor metálica é 1,8 vez maior que a de adquirir um carro de cor sólida e sabendo que, em determinado período, dois carros foram comprados, nessa concessionária, de forma independente, julgue os itens a seguir.

A probabilidade de que somente um dos dois carros comprados seja de cor metálica é superior a 50%.

• C. Certo
• E. Errado

Em um baralho de 52 cartas há 13 cartas de cada naipe (paus, copas, espadas e ouros). Escolhendo de maneira aleatória 5 cartas, qual a probabilidade de elas serem do mesmo naipe?

• A.

  

• B.

  0,20

• C.

  

• D.

  

• E.

  

Considere o lançamento, de maneira independente, de dois dados honestos com 6 faces, numerados de 1 a 6, e considere A o evento cuja soma das duas faces seja par, e B, o evento cujo módulo da subtração das faces seja igual a 1. Dado que o evento B não ocorreu, qual a probabilidade de A ocorrer?

• A.

  20/36

• B.

  18/36

• C.

  10/36

• D.

  0

• E.

  12/36