Questões sobre Probabilidade

Considere o espaço amostral formado por números inteiros de 1 a 20. Sejam A, B e C subconjuntos deste espaço amostral, onde A é o conjunto dos números primos, B, o conjunto dos números pares, e C o conjunto dos múltiplos de 3. O conjunto 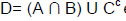é dado por

• A.

  {2,4,6,8,10,12,14,16,18,20}

• B.

  {2,3,6,7,9,11,12,13,15,17,18,19}

• C.

  Apenas o conjunto C^c

• D.

  Todo o espaço amostral

• E.

  {2,3,6,7,11,13,17,19}

Três máquinas A, B e C produzem respectivamente 40%, 50% e 10% do total de peças de uma fábrica. As porcentagens de peças defeituosas nas respectivas máquinas são 10%, 5% e 8%. Uma peça é sorteada ao acaso. Dado que a peça é boa, qual a probabilidade de ter vindo da fábrica A?

• A.

  0,4

• B.

  135/873

• C.

  54/1281

• D.

  360/927

• E.

  40/73

Com relação ao problema da questão anterior, selecionando uma peça ao acaso, qual a probabilidade de a peça ser defeituosa?

• A.

  11/100

• B.

  10/23

• C.

  1/23

• D.

  73/1000

• E.

  11/76

Sejam A e B dois eventos independentes, então NÃO podemos afirmar que:

• A.

  A e B são disjuntos;

• B.

  a probabilidade da interseção entre A e B é a multiplicação das probabilidades;

• C.

  A é independente do complementar de B;

• D.

  o complementar de A é independente do complementar de B;

• E.

  P(A U B)=P(A)[1-P(B)]+P(B).

Supondo que a taxa de acidentes é igual para qualquer hora do dia, qual a probabilidade de haver dois ou mais acidentes em uma hora?

• A.

  48²e^–48/2

• B.

  1– 3 e^–2

• C.

  1– 48²e^–48/2

• D.

  1– 49e^–48

• E.

  4 e^–2

Com relação a Cadeias de Markov, considere a seguinte matriz de transição, com as seguintes probabilidades de sair do estado x e chegar a y, em 1 passo.

Em relação aos tipos de estado, podemos dizer que:

• A.

  os estados 2 e 3 formam um conjunto absorvente;

• B.

  os estados 1 e 3 são transientes;

• C.

  o estado 0 é recorrente;

• D.

  apenas o estado 2 é absorvente;

• E.

  não existe nenhum estado recorrente.

Com relação à matriz do item anterior, a probabilidade de sair do estado 0 e chegar ao estado 3, em dois passos é:

• A.

  0

• B.

  0,6

• C.

  0,42

• D.

  0,24

• E.

  0,44

Considere uma distribuição conjunta de duas variáveis contínuas X e Y, dadas pela função de densidade f(x,y)=x+y, 0<x<1,0<y<1. A densidade marginal de X é dada por:

• A.

  f(x)=x, 0<x<1

• B.

  f(x)=x-1, 0<x<y

• C.

  f(x)=x+1/2, 0<x<1

• D.

  f(x)=1+x, 0<x<1

• E.

  f(x)=x, y<x<1

• A.

  0,75

• B.

  0,70

• C.

  0,50

• D.

  0,45

• E.

  0,40

Dez participantes de um programa de televisão serão distribuídos aleatoriamente em duas casas, sendo que, em cada casa, haverá o mesmo número de participantes, isto é, 5 em cada uma. Desses 10 participantes, 3 preferem a casa X e 2 preferem a casa Y. Qual é a probabilidade de as preferências serem atendidas?

• A.

  

• B.

  

• C.

  

• D.

  

• E.