Questões sobre Probabilidade
Lista completa de Questões sobre Probabilidade para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Seja (X,Y) uma variável aleatória bidimensional distribuída uniformemente sobre a região R = {y > 0, 0 < x < 1, x + y < 1}. A probabilidade P(Y < 3X) vale
- A.

- B.

- C.

- D.

- E.


- A.

- B.

- C.

- D.

- E.

Sejam X e Y duas variáveis aleatórias contínuas, com funções de densidade marginais fX(x) e fY(y), respectivamente, e função de densidade conjunta fX,Y(x,y). As variáveis X e Y são independentes se
- A.
fX,Y(x,y) = fX(x) fY(y)
- B.
fX,Y(x,y) = 0
- C.
E(XY) = E(X)E(Y)
- D.
X e Y têm distribuições normais
- E.
a correlação entre X e Y é igual a zero

- A.
I e II
- B.
I e III
- C.
II e IV
- D.
III e IV
- E.
I, II e IV

- A.

- B.

- C.

- D.

- E.

Dentre os calouros de uma Universidade, 30% cursam ciências exatas, 40% cursam ciências humanas e 30% cursam ciências biológicas. As porcentagens dos que desistem do curso no 1o ano são dadas por 10%, 5% e 10%, respectivamente, para os alunos de exatas, humanas e biológicas. Dois calouros são selecionados aleatoriamente e com reposição dentre todos os calouros dessa Universidade. A probabilidade de exatamente um desistir do curso no 1o ano é
- A.
0,0736
- B.
0,0842
- C.
0,1472
- D.
0,1684
- E.
0,1864
Julgue os itens a seguir, relativos ao cálculo de probabilidades.
A relação 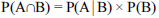 é válida somente se A e B forem eventos independentes.
é válida somente se A e B forem eventos independentes.
- C. Certo
- E. Errado
Uma empresa iniciou suas atividades com R$ 30 mil de capital. O custo fixo mensal da empresa é de R$ 5 mil. As vendas de seus produtos ocorrem segundo um processo de Poisson, com taxa igual a R$ 1 mil por mês. A empresa fechará no momento que o seu capital for igual ou inferior a zero. Com base nessa situação, e considerando exp( 6) = 0,0025, julgue o item seguinte.
A probabilidade de a empresa sobreviver além do sexto mês de funcionamento é inferior a 0,95.
- C. Certo
- E. Errado
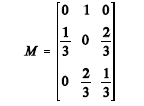
A matriz M mostrada acima representa a matriz de transição de um processo de Markov, cujos estados 1, 0 e +1, representam a situação de um apostador por jogada. Para jogar, o apostador deve pagar R$ 1,00. Ao final de cada jogada, ele pode perder o valor apostado (1), ou ele pode recuperar o valor apostado (0), ou ele pode obter lucro (+1). Com base nessas informações, julgue o item abaixo.
Ao final da segunda jogada, o lucro esperado desse apostador será negativo.
- C. Certo
- E. Errado
Uma unidade fracionadora de líquido de gás natural que hoje está funcionando perfeitamente pode, amanhã, apresentar uma pequena avaria (que a permita continuar operando), com probabilidade 0,3, ou quebrar completamente, sem possibilidade de conserto, com probabilidade 0,2. Por outro lado, se a unidade apresenta hoje uma pequena avaria, a probabilidade de que amanhã ela esteja totalmente quebrada é 0,7. Suponha que o processo estocástico que descreve o estado da unidade (perfeita, levemente avariada ou completamente quebrada) seja uma cadeia de Markov homogênea. Se a unidade está perfeita em determinado dia, a probabilidade de que ela esteja completamente quebrada dois dias depois é
- A. 0,10
- B. 0,21
- C. 0,24
- D. 0,31
- E. 0,51


